Internet Encyclopedia of Science
SOLIDS & SURFACES
A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  W  X  Y  Z

                   • HOME
• ABOUT
• CATEGORIES
• USE OF TEXT AND IMAGES
• NEWSLETTER

  



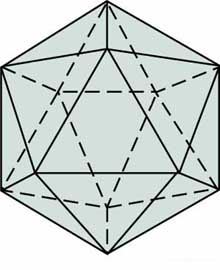
icosahedron


icosahedron
A polyhedron with 20 faces. A regular icosahedron has faces that are all equilateral triangles, and is one of the five Platonic solids. The length from vertex to opposing vertex of a regular icosahedron is 51/4 φ1/2 d where φ (phi) is the golden ratio and d is the length of the side of one of the triangular faces. Chopping off each vertex (corner) of a regular icosahedron reveals the 12 pentagonal and 20 hexagonal faces of the truncated icosahedron, which is one of the 13 Archimedean solids (shapes made from truncating Platonic solids in certain ways).

In chemistry, icosahedral units are found in many boron derivatives, e.g. B12H122-.


Related entry

   • Icosian Game


Related category

   • SOLIDS AND SURFACES


Also on this site:

Encyclopedia of Alternative Energy & Sustainable Living
Encyclopedia of History




BACK TO TOP