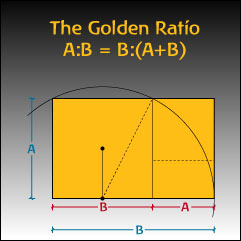
The golden ratio (φ) is a remarkable number that, like pi and e, pops up all over the place in mathematics but, in some ways, has a more 'human' connection in that it seems to be linked to aesthetics. Its name, which is also given as the golden mean, the golden section, the golden number, and the divine proportion, reflects this sense of a harmonious or pleasing ideal.

 

The golden ratio is an irrational number of the type known as an algebraic number (in contrast with pi and e, which are transcendental) and is represented by the Greek letter φ (phi). It can be defined in various ways. For example, it is the only number equal to its own reciprocal plus 1, i.e. φ = (1/φ so that φ² = φ + 1. From this comes the quadratic equation φ² – φ – 1 = 0 of which the golden ratio is the positive solution, (1 + √(5))/2 = 1.6180339887... The golden ratio is also approximated by the ratio of successive terms in the Fibonacci sequence; in fact, F(n+1)/F(n) gets closer and closer to phi as n tends to infinity. Because 1/(1 – φ) = φ, the continued fraction representation of φ is

 

φ = 1+1/(1+1/(1+1/(1+1/(1+1/... = [1;1,1,1,1, ...]

 

Two quantities are said to be in the golden ratio, if the ratio of the larger one, a, to the smaller one, b, is the same as the ratio of the smaller one to their difference, i.e., a/b = b/(a – b). The so-called golden rectangle is one whose sides a and b stand in the golden ratio. It is famously said to have great aesthetic appeal and is closely approximated by the dimensions of the front of the Parthenon in Rome. Leonardo da Vinci's masterpiece the Mona Lisa is said to have a face that is framed by a golden rectangle; what is certain is that Leonardo was a close personal friend of Luca Pacioli, who published a three-volume treatise on the golden ratio, Divina Proportione, in 1509. The Swiss-French architect and painter Le Corbusier designed an entire proportional system called the "Modulor," that was based on the golden ratio. The Modulor was supposed to provide a standardized system that would automatically confer harmonious proportions to everything, from door handles to high-rise buildings. Another artist who deliberately used the golden ratio is the surrealist Salvador Dali. The ratio of the dimensions of Dali's Sacrament of the Last Supper is equal to the golden ratio. Dali also incorporated in the painting a huge dodecahedron (a twelve-faced Platonic solid in which each side is a pentagon) engulfing the supper table.

 

The dodecahedron, which according to Plato is the solid "which the god used for embroidering the constellations on the whole heaven," is intimately related to the golden ratio – both the surface area and the volume of a dodecahedron of unit edge length are simple functions of the golden ratio. In fact, φ turns up frequently in figures that have pentagonal symmetry. For instance the ratio of a regular pentagon's side and diagonal is equal to φ, and the vertices of a regular icosahedron are located on three orthogonal golden rectangles. The golden ratio is also related to Penrose tiling and to the plastic number.

 

Reference

1. Livio, Mario. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. New York: Broadway Books, 2002.