A strophoid is a looping curve, first studied in 1670 by Isaac Barrow, the first Lucasian professor of mathematics at Cambridge and the immediate predecessor of Isaac Newton in this job. The strophoid, which is a special case of the general cissoid, was named by Montucci in 1846 from the Latin for "twisted belt shape."

 

 

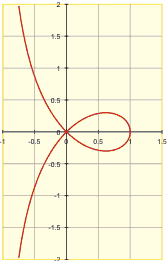The elaborate rules for drawing a strophoid are as follows. Let C be a curve, let O be a fixed point called the pole, and let O' be a second fixed point. Let P and P' be points on a line through O meeting C at Q such that P'Q = QP = QO'. The locus of P and P' is the strophoid of C with respect to the pole O and fixed point O'. If the curve C is a straight line, the pole P is not on C, and the second point O' is on C, the resulting strophoid is called an oblique strophoid. If these same conditions apply except that O' is the point where the perpendicular from O to C cuts C then the strophoid produced is called a right strophoid. On the other hand if C is a circle, O is the center of the circle, and O' a point on its circumference, then the strophoid that results is known as Freeth's nephroid.

 

The French mathematician Gilles Roberval (1602–1675) found the strophoid in a different way – as the result of planes cutting a cone. When the plane rotates (about the tangent at its vertex) the collection of foci of the obtained conics gives the strophoid.