capacitance
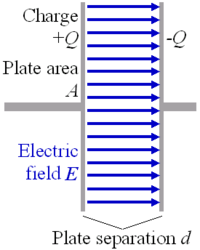
Parallel-plate capacitor.
Capacitance is a measure of the amount of electric charge separated for a given electric potential (V). If equal and opposite charges are put on the conductors of a capacitor (a device consisting of two conductors closely separated by an insulating medium), then the capacitance (C) is given by
C = Q/V
where Q is the charge on one of the plates.
The SI unit of capacitance is the farad. This is much larger than the capacitance of most capacitors found in electronic circuits, so that in practice the units commonly used are the millifarad (mF), microfarad (μF), nanofarad (nF), and picofarad (pF).
Separation versus storage of charge
Often capacitance is said to be a measure of the ability of a capacitor to store charge. In fact, a charged capacitor has zero net charge. The process of "charging" a capacitor involves putting a charge Q on one conductor and -Q on the other. Therefore, it's more accurate to say that there has been a separation of charge, brought about by the movement of charge from one conductor to the other.
The capacitance of a solitary object, such as an isolated sphere, is determined by considering the other conductor to be an infinite sphere surrounding it. The object is given charge by moving charge from the infinite sphere, which acts as an infinite charge reservoir ("ground"). The potential of the object is the potential between the object and the infinite sphere.
Capacitors
Capacitance depends only on the geometry of the capacitor's physical structure and the relative permittivity (εr ) of the material medium in which the capacitor's electric field exists. The size of the capacitor's capacitance is the same whatever the charge and potential (assuming the dielectric constant doesn't change). This is true even if the charge on both conductors is reduced to zero. If a capacitor with charge on its conductors has a capacitance of, say, 2 μF, then its capacitance is also 2 μF when the conductors have no charge.
Capacitance is directly proportional to the area A of either conductor and indirectly proportional to the distance d between the conductors. In the case, of a parallel-plate capacitor:
C = εr A / 4πd.
Energy of a charged conductor
The operation of assembling upon a conductor a group of charges that mutually repel one another requires work and therefore results in the production of potential energy. It is customary to say that this potential energy is possessed by the charged conductor itself although, it may be more correct to picture the energy as stored in the field surrounding the conductor.
The amount of this stored energy can be calculated by considering the charging operation as a piecemeal affair in which the final charge is built up of small increments. Let us suppose that at some stage during this operation the conductor has a total charge Q'. Its potential is then
V' = Q'/C' (1)
Since equation (1) represents the work involved in bringing a unit charge to the surface of the Q'-charged conductor, that required to deposit an increment of charge dQ' is
dW = V'dQ' = Q'dQ'/C (2)
The total work to attain the final charge Q is
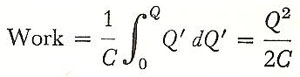
Work = CV 2/2
Work = QV/2


