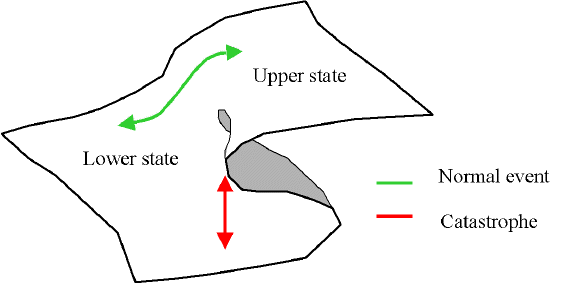
Catastrophe theory is a theory, developed by the French mathematician René Thom (1923–2003), that attempts to explain the behavior of complex dynamical systems by relating it to topology. The evolution of such systems consists of steady continuous change interspersed with sudden major jumps, or "catastrophes," when the topology of the set changes.

 

Catastrophe theory has been applied, with varying degrees of success, to phenomena as diverse as earthquakes, stock market crashes, prison riots, and human conflicts, at the personal, group, and societal level. The theory was first developed by Thom in a paper published in 1968 but became well known through his book Structural Stability And Morphogenesis (1972).¹ Many mathematicians took up the study of catastrophe theory and it was in tremendous vogue for a while, yet it never achieved the success that its younger cousin chaos theory has because it failed to live up to its promise of useful predictions.

 

Late in his career, the surrealist Salvador Dali painted Topological Abduction Of Europe: Homage To René Thom (1983), an aerial view of a seismically fractured landscape juxtaposed with the equation that strives to explain it.

 

Reference

1. Thom, R. Structural Stability and Morphogenesis: An Outline of a General Theory of Models. Reading, Mass.: Addison-Wesley, 1993.