circular motion
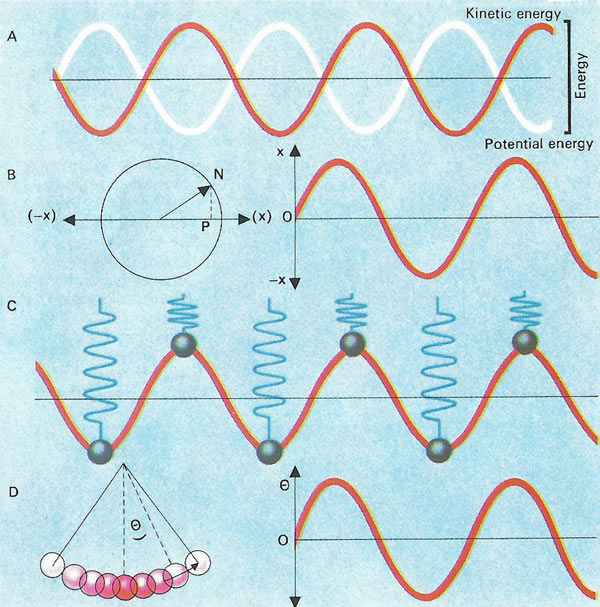
All periodic motion involves the continuous interchange of kinetic and potential energy, as shown in the graph [A]. Simple harmonic motion (SHM) is one form of periodic motion that is characterized by the shape of a sine wave [B]. The point [P] on the diameter of the circle around which N is moving is an example of SHM. The mass on a spring [C] performs linear SHM and a pendulum [D] performs angular SHM.
When a stone is tied to the end of a string and whirled round in a circle at constant speed, the velocity's magnitude is unchanged but the direction alters continuously. If the string were cut at any instant, the stone would fly off along a tangent to the circle (as seen in the sparks flying off a rotating Catherine-wheel).
A force must be acting on the rotating stone to produce its acceleration. Here the force is due to the tension in the string and one can feel this force on the hand as the stone is whirled round. It is called the centripetal force because it acts toward the center of the circle. The acceleration it produces is therefore similarly directed toward the center. For a car moving round a circular track, frictional forces at the ground acting on the wheels provide the centripetal force.
Newton's laws are only applicable to non-accelerating frameworks. For these laws to hold true in the accelerating framework of a rotating system, we must introduce centrifugal force as a fictitious force acting outward from the orbit center. The effect of this force is used in the domestic spin-drier to squeeze the water out of wet laundry and, on a larger scale, in the centrifuges that whirl astronauts and pilots to the high acceleration forces encountered in flight.
Circular velocity
Circular velocity is the horizontal velocity of an object required to keep it in a circular orbit at a given altitude about a planet or other gravitating mass. It is given by √[G(M + m)/R], where G is the gravitational constant, M is the mass of the central body, m is the mass of the orbiting body (which can be ignored, for example, in the case of an orbiting spacecraft), and R is the distance separating the orbiter from the center of the gravitating body.
Periodic motion
Both centripetal and centrifugal forces depend on the mass (m) of the object and its velocity (v) in the circular motion (circle of radius r). A heavy object needs a greater centripetal force to hold it in orbit and a greater force is also required for high speeds of rotation. Experiment shows that, in addition, the required force (F) is inversely proportional to the radius of motion, and F = mv2/r where v 2/r gives the magnitude of the centripetal acceleration.
Uniform circular motion is periodic – that is, the events recur over and over again. The time taken for a complete revolution of the object remains constant. This periodic character is further demon started by considering how the object's distance from any fixed diameter of the circle varies with time. If a graph of these distances is plotted, the resulting curve is one of a uniformly oscillating displacement, resembling a sine wave.
For a swinging pendulum, the force which pulls the bob back through the central vertical position is its weight. It undergoes oscillatory motion with an acceleration that is proportional to its distance from the point of suspension and it is also directed toward that point. Movement of this type is called simple harmonic motion and for the pendulum the time taken for a complete cycle of forwards and backwards swing (the oscillation period t) is proportional to the square root of its length (l). The number of cycles completed per second is called the frequency of oscillation (measured in hertz).
The displacement in all types of simple harmonic motion rises and falls like a sine wave. Many other wave motions behave in this way. If a long rope is clamped at one end and its free end is whipped, a wave-like disturbance travels along the rope and the amplitude of the rope's displacements at any point from the fixed end is described by the waveform shown in the illustration below.


