simple harmonic motion
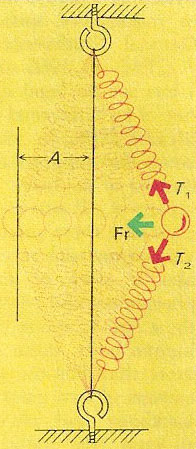
Hypothetical example of simple harmonic motion. A body is suspended on springs midway between two hooks. The body is displaced from its equilibrium position, taking care that it remains equidistant from both hooks. If gravitational effects are ignored, the body will described an SHM about the midline when it is released. The force (F1) toward the center of motion is the resultant of the components toward the midline of the tensions (T1, T2) in the springs. Undamped, the motion will continue indefinitely, potential energy in the springs being converted to kinetic energy in the motion of the body as the body approaches the midline, and the reverse occurring as the body approaches its maximum amplitude (A) again. The graphical expression of the motion, displacement (y) against time (t ), is shown in the diagram above. It is the graph of.
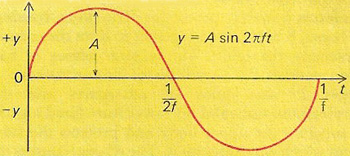
The graphical expression of the motion, displacement (y) against time (t ), is shown in the diagram above. It is the graph of y = A sin2πft, where f is the frequency of the motion.
Simple harmonic motion (SHM) is a form of wave motion in which a moving particle traces a path symmetric about a midpoint or equilibrium position, through which it passes at regular intervals of time. A particle is said to move in simple harmonic motion when it oscillates along a line about a central or equilibrium point, O, so that its acceleration towards O is always proportional to its distance from O. Thus, if a point P moves in a circle, center O and radius r, with a constant angular velocity ω, the projection of P on any diameter will move in simple harmonic motion. If the distance from O of the projection of P on a vertical diameter is y, at time t, then a graph of y against t will give a sine wave of amplitude r and equation y = r sinωt. This equation may be rewritten in the more general form:
y = r sin2π (t /T – x/λ)
where T is the period of the wave, λ its wavelength and x the distance it has traveled from O in time t.
Simple harmonic motion derives its name from the fact that the vibrations produced by musical instruments (e.g., a string of a violin, the legs of a tuning fork), and hence the sound waves they propagate, approximate to it. In fact these, as all other vibrations and wave motions, may be treated as compounded of a number of SHMs.


