Davisson and Germer experiment

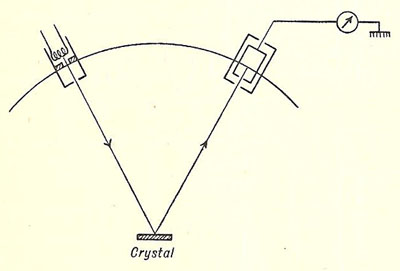
Simplified diagram of the Davisson and Germer experiment
Source: Introducing Atomic Physics, Samuel Tolansky (1956)

A series of experiments carried out by the American physicists Clinton Davisson and Lester Germer in 1927, which provided the first experimental support for Louis de Broglie's bold hypothesis that particles of matter have wave properties (see de Broglie and matter waves). Electrons from a heated filament were accelerated by a small potential difference and allowed to impinge upon a single crystal of nickel. The intensity of the electrons was measured for various angles of scattering for a range of accelerating potentials from 40 to 68 volts. For electrons accelerated through 54 volts the reflection was most pronounced and occurred at an angle of 50° to the incident electron beam.

Bearing in mind that the kinetic energy of the electrons is given by ½mv² = Ve and that the wavelength associated with them is h/mv, the wavelength is given by λ = h/√(2Vem). Substitution of relevant data gives

λ = (6.6 × 10^-34/√(2 × 54 × 1.6 × 10^-19 × 9.1 × 10^-31) = 1.67 × 10^-10 m = 0.167 nm.

This wavelength is in the X-ray range. X-rays had already provided information about the spacing of the atomic planes in the nickel crystal, and it is therefore a simple matter to use the Bragg formula (see Bragg's law) to calculate the wavelength of the scattered electrons. As the angle of scattering is 5o°, the angles of incidence and reflection must each be 25°. This implies that the reflecting planes in the crystal are inclined at 25° to the top surface of the crystal. The distance d between the reflecting crystal planes is d = 215 sin 25° = 90.9 pm. Using the Bragg formula mλ = 2d sin θ we get &lambda = 2 × 90.9 sin 65° = 165 pm. Agreement between the measured and predicted wavelength is therefore established.

Related category

• ATOMIC AND NUCLEAR PHYSICS

Also on this site:

Encyclopedia of Alternative Energy & Sustainable Living
Encyclopedia of History

BACK TO TOP