Devil's curve

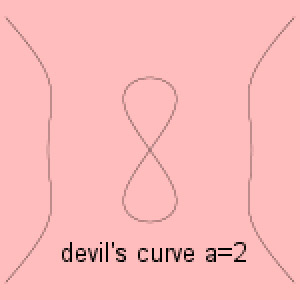
Image: Jan Wassenaar
www.2dcurves.com

Also known as the Devil on Two Sticks, a curve with the Cartesian equation

y⁴ - a²y² = x⁴ - b²x²

and the polar equation

r²(sin²θ - cos²θ) = a²sin²θ - b²cos²θ.

Early studies of it were carried out in 1750 by the Swiss mathematician Gabriel Cramer (1704–1752), who is most famous for his work on determinants, and in 1810 by Lacroix. For a = 25/24, the curve is called the electric motor curve.

Related category

• PLANE CURVES

Also on this site:

Encyclopedia of Alternative Energy & Sustainable Living
Encyclopedia of History

BACK TO TOP