Diophantine equation
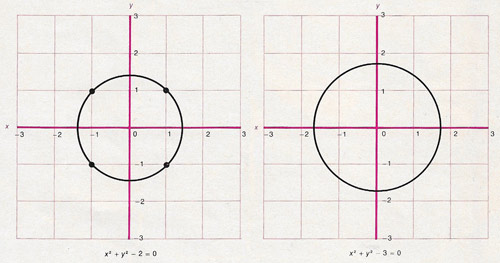
Graphs of two equations illustrate the difference between an ordinary equation and a Diophantine equation, for which one is interested only in whole-number solutions; this difference is central to Hilbert's 10th problem. The equations in question are x 2 + y 2 – 2 = 0 (left) and x 2 + y 2 – 3 = 0 (right); both are represented by circles with their center at the origin, that is, at the point with coordinates x = 0, y = 0. In the case of x 2 + y 2 - 2 = 0 the circle has a radius of √2. If the equation is treated as an ordinary equation, there are infinitely many solutions. If, however, it is treated as a Diophantine equation, there are only four solutions: (1) x = 1, y = 1, (2) x = –1, y = 1, (3) x = 1, y = –1, and (4) x = –1, y = –1. These solutions are represented by dots where the graph crosses the four points with those coordinates on the Cartesian grid. In the case of x 2 + y 2 – 3 = 0, the circle has a radius of √3. As an ordinary equation it has an infinite number of solutions; as a Diophantine equation, however, it has none at all.
A Diophantine equation is an equation that has integer coefficients and for which integer solutions are required. Such equations are named after Diophantus. The best known examples are those from Pythagoras's theorem, a 2 = b 2 + c 2, when a, b, and c are all required to be whole numbers – a so-called Pythagorean triplet. Despite their simple appearance Diophantine equations can be fantastically difficult to solve. A notorious example comes from Fermat's last theorem (recently solved), a n = b n + c n for n > 2.
To give a specific example, suppose we want to find integer values for x and y such that
x 2 = 1620y 2 + 1.
A trial and error approach using a computer would quickly find the solution: y = 4, x = 161. However, just a slight change to the equation to make it
x 2 = 1621y 2 + 1
would leave the trial and error method floundering, even with the resources of the most powerful computers on Earth. The smallest integer solution to this innocent looking formula involves a y-value that is on the order of a thousand trillion trillion trillion trillion trillion trillion!
One of the challenges (the tenth one) that David Hilbert threw down to 20th-century mathematicians in his famous list was to find a general method for solving equations of this type. In 1970, however, the Russian mathematician Yuri Matiyasevich showed that there is no general algorithm for determining whether a particular Diophantine equation is soluble: the problem is undecidable. 1, 2
References
1. Matijasevic, Yu. V. "Solution of the Tenth Problem of Hilbert." Mat.
Lapok, 21: 83- 87 (1970).
2. Matijasevic, Yu. V. Hilbert's Tenth Problem. Cambridge, Mass.:
MIT Press, 1993.


