Henry Dudeney was an English writer and puzzle-maker who became one of the greatest exponents of recreational mathematics of his time. Chess and chess problems captivated him from an early age and he was only nine when he started contributing puzzles to a local newspaper. His education was limited and he started work as a clerk in the civil service at the age of 13. However, he kept up his interest in math and chess, wrote articles for magazines under the pseudonym "Sphinx," and joined a literary circle that included Arthur Conan Doyle.

 

In 1893 Dudeney struck up a correspondence with the American puzzle-maker Sam Loyd, the other leading mathematical recreationist of the day, and the two shared many ideas. However, a rift developed after Dudeney accused Loyd of publishing many of Dudeney's puzzles under his own name. One of Dudeney's daughters "recalled her father raging and seething with anger to such an extent that she was very frightened and, thereafter, equated Sam Loyd with the devil."

 

Dudeney was a columnist for the Strand Magazine for over 30 years and wrote six books. The first of these, The Canterbury Puzzles,¹ published in 1907, purports to include a collection of problems posed by the characters in Chaucer's The Pilgrims' Progress. The answer to the so-called haberdasher's puzzle is Dudeney's best known geometrical discovery. His other books include Amusements in Mathematics (1917)² and The World's Best Word Puzzles (1929).³

 

Haberdasher's puzzle

 

 

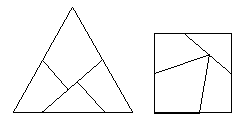The haberdasher's puzzle is to cut an equilateral triangle into four pieces that can be rearranged to make a square. It was the greatest mathematical discovery of Henry Dudeney and published by him, first in the Weekly Dispatch in 1902 and then as problem no. 26 in The Canterbury Puzzles (1907). The diagram above shows the solution, which, in his book, Dudeney describes as follows:

 

Bisect AB in D and BC in E; produce the line AE to F making EF equal to EB; bisect AF in G and describe arc AHF; produce EB to H, and EH
is the length of the side of the required square; from E with distance EH, describe the arc HJ, and make JK equal to BE; now from the points D and
K drop perpendiculars on EJ at L and M.

 

A remarkable feature of the solution is that the each of the pieces can be hinged at one vertex, forming a chain that can be folded into the square or the original triangle. Two of the hinges bisect sides of the triangle, while the third hinge and the corner of the large piece on the base cut the base in the approximate ratio 0.982: 2: 1.018. Dudeney showed just such a model of the solution, made of polished mahogany with brass hinges, at a meeting of the Royal Society on May 17, 1905.

 

References

1. Dudeney, H. E. The Canterbury Puzzles. London: Nelson, 1907. Reprinted Mineola, NY: Dover, 1958.
2. Dudeney, H. E. Amusements in Mathematics. New York: Dover, 1917. Reprinted Mineola, NY: Dover, 1958.
3. Dudeney, Henry E. The World's Best Word Puzzles. London: Daily News, 1925.
4. Dudeney, H. E. 536 Puzzles and Curious Problems, ed. by Martin Gardner. New York: Charles Scribner, 1967
5. Newing, Angela. "The Life and Work of H. E. Dudeney." MS, 21: 37-44 (1988- 1989).