A polyomino is a two-dimensional shape made by connecting n squares of the same size along their edges. The polyomino is a generalization of the domino, which can be thought of as a polyomino with n = 2.

 

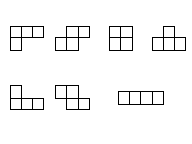There are 5 distinct tetrominoes. (Of the 7 arrangements shown here, two pairs are reflections.)

An X-pentomino is a five-square polyomino in the shape of the letter X.

 

Several puzzles involving polyominoes made from three or more squares stuck together became popular around the beginning of the twenieth century. The best-known of these is the Broken Chessboard, presented as problem no. 74 in Henry Dudeney's book The Canterbury Puzzles (1907). Dudeney gives an amusing introduction to the problem, first quoting from Hayward's Life of William the Conqueror (1613) about an incident in which Prince Henry, one of William's sons, smashes a chessboard over the head of his brother, Prince Robert, and then adding his own mathematical appendix. By a curious quirk, Dudeney reveals, the board breaks into 13 pieces, 12 of which are the different possible ways in which five squares can be arranged and one square 2 × 2 piece. The puzzle is to reconstitute the board from these fragments. This is the earliest example of a mathematical recreation that involves pentominoes, a name that wasn't coined until 1953 when Solomon Golomb first used it in a talk to the Harvard Math Club. Golomb not only invented the nomenclature for polyominoes but did much of the pioneering research on them. His work was brought to a wide audience and popularized by Martin Gardner in his Scientific American column, beginning in 1957.^{1, 2, 3}

 

Golomb was particularly interested in the pentomino, for a reason that becomes clear from the table shown below ("Types of Polyomino"). The familiar domino comes in just one configuration as, obviously, does the trivial monomino. A triomino can have two different shapes – three squares in a line or in an L shape. The tetromino (or tetramino) has five distinct arrangements (i.e. arrangements that are not reflections or rotations of each other) and is used in the popular video game Tetris. Thus for n ≤ 4 the number of distinct pieces is ≤ 5, which restricts the variety of combinations possible. On the other hand, for n > 5, the number of different pieces is large, making analysis of problems difficult and games based on such polyominoes difficult and unwieldy. However, pentominoes, for which n = 5, come in 12 unique configurations, which is just about an ideal balance between tractability and combinatorial richness, hence the high level of interest in this particular type of polyomino. The problem of tiling an 8 × 8 chessboard with a square hole in the center using pentominoes was first solved in 1935 and found, by computer in 1958, to have exactly 65 solutions. Another standard pentomino puzzle is to arrange the set of 12 possible shapes into a rectangles without holes: 3 × 20, 4 × 15, 5 × 12, and 6 × 10.

 

Pentominoes are prominently featured in a subplot of the novel Imperial Earth by Arthur C. Clarke. Australian puzzlist Kate Jones (of Kadon Enterprises), who has contributed much to the lore of pentominoes herself since being introduced to them through Clarke's novel, points out that in Blue Balliett's best-selling children's mystery books, Chasing Vermeer¹ and The Wright 3, pentominoes feature significantly in the plots.

 

Hexominoes and heptominoes come in 35 and 108 unique arrangements, respectively. One of the 108 heptomino configurations, however, has a hole – a region that is not tiled with squares but that is unconnected to the exterior of the polyomino – and may or may not be counted as a valid piece depending on the rules of a particular game. All polyominoes made of seven or more squares may contain holes. There is no known algorithm or formula for calculating how many distinct polyominoes of each order there are.

 

Related to polyominoes are polyiamonds (formed from equilateral triangles) and polyhexes (formed from regular hexagons). The three-dimensional analog of polyominoes uses cubes instead of squares; an example is the Soma Cube.

 

Types of polyomino
name	no. of unit squares	no. of distinct configurations
monomino	1	1
domino	2	1
triomino	3	2
tetromino	4	5
pentomino	5	12
hexomino	6	35
heptomino	7	108

 

References

1. Gardner, M. New Mathematical Diversions from Scientific American. New York: Simon and Schuster, 1966.
2. Golomb, S. W. "Checker Boards and Polyominoes." Amer. Math. Monthly, 61: 675–682 (1954).
3. Golomb, Solomon W. Polyominoes: Puzzles, Patterns, Problems, and Packings. New York: Charles Scribner's, 1965. (2nd ed. Princeton, NJ: Princeton University Press, 1995.)
4. Jones, Kate. On-line review of Chasing Vermeer.