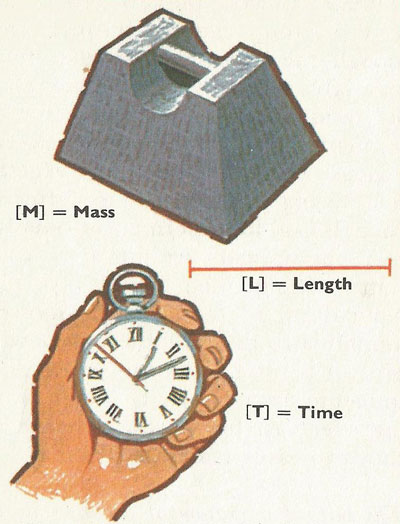
The three dimensions in physics are mass, length, and time. The basic units, common to all branches of physics, are also the units of mass, length, and time. All other kinds of units are derived units: analysis shows that, however involved the unit, whether it is a unit of force, viscous drag, heat, or even electric charge, it can still be broken down into an expression (or a function) involving mass, length, and time.

 

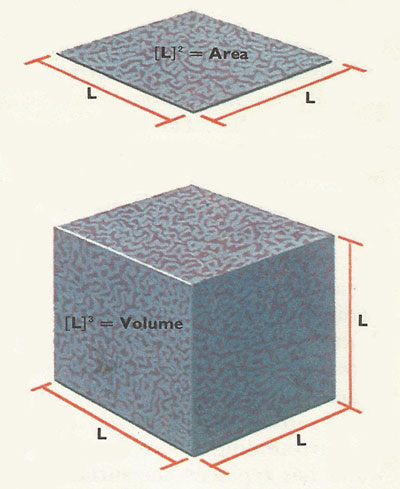
The unit of area is a square unit, or a length multiplied by a length. Area has the dimensions of length [length] ². Volumes are measured in cubic units – a length multiplied by a length multiplied by a length. The dimensions of volume are therefore [length] ³. (Square brackets are always used to denote dimensions.) The dimensions of mass, length, and time are symbolized by [M], [L], and [T].

 

The unit of density is the kilogram per cubic meter, so it has the dimensions of [mass] divided by [length]³.

 

[density] = [M] / [L] ³

 

Or, alternatively

 

[density] =[M] × [L]^–3

 

Whenever index numbers, for example the square index number 2 or the cube index number 3, appear 'under the line' as the divisor, it is exactly equivalent to minus the same index number on top of the line. The unit of acceleration is the meter per second or

 

[acceleration] = [L] / [T] ²

 

but it can also be written as [L] [T] ^–2. The multiplication signs are usually omitted. When the dimension is just [L], [M], or [T], it is the same as [L]¹, [M]¹, or [T]¹.

 

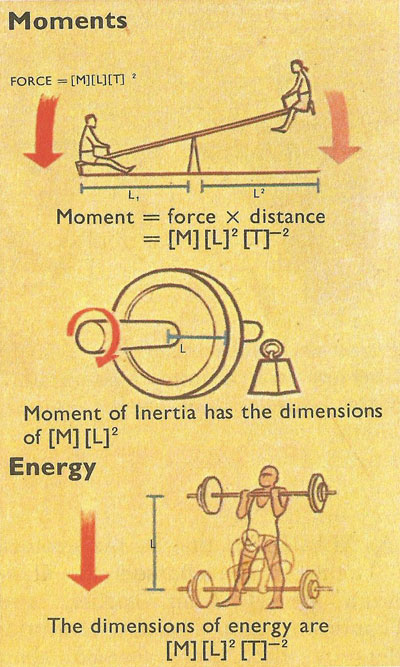
The dimensions of force are particularly important because forces have to be considered in all branches of physics. The dimensions can be derived from [mass] and [acceleration]. Force is equal to mass multiplied by acceleration, so

 

[force] = [M] [L] [T] ^–2.

 

The dimensions of force lead on to the dimensions of energy, another unifying quality, since it appears in every branch of physics. Energy in dynamics is a force multiplied by a distance. The dimensions of energy must be identical, wherever it appears, so

 

[energy] = [force] × [distance] = [M] [L] [T] ^–2 × [L]

 

This expression can be simplified, because the two dimensions of length can be collected together

 

[L] × [L] = [L] ²,

 

which demonstrates one of the useful properties of the indices. To multiply, simply add the indices; to divide, subtract.

 

In mathematics, equations have just numbers (or symbols, like x and y, which represent unknown numbers) on either side. Unknown quantities appear in equations, in physics, but there is the additional proviso that the indices of dimensions must be identical on both sides of the equation. It is no use equating a force on one side of an equation to energy on the other side – the dimensions are different. If the dimensions are different on either side the answer will inevitably be wrong.

 

One of the equations of motion is written as

 

s = u t + ½ at ²

 

where s is distance, u is velocity, a is acceleration, and t is time. A quick check shows that the dimensions are correct. The left hand side of the equation has the dimensions of length, so each of the parts on the right hand side must also have the dimensions of length.

 

[ut] = [velocity] × [time] = [L] [T] ^–1 × [T]

 

[T] and [T]^-1 cancel each other out, leaving only [L].

 

at ² = [acceleration] × [time] ² = [L] [T] ^-2 × [T] ² = [L].

 

So the whole equation is dimensionally in order.

 

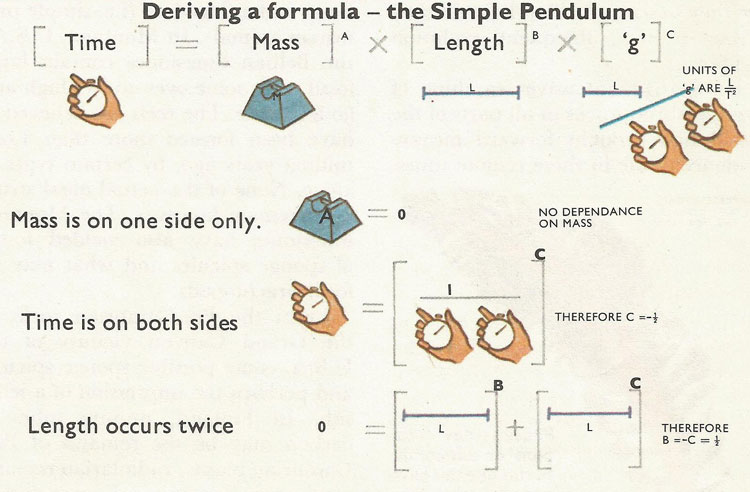
But perhaps the most useful quality of dimensions is that they can be used to derive quite involved formulae. No knowledge of the dynamics of oscillations is required to work out how the period of a simple pendulum depends on its length, and the pull of gravity. The method of dimensions gives the relationship in a simple and elegant way.

 

What can the period depend on? Commonsense suggests that it may depend on the mass and length of the pendulum, and also on g, the acceleration due to Earth's gravity. But does it depend on (mass)² or the square root of mass ((mass)½)? Could it be the (length)², or simply (length)? And how does g enter the relationship? The index of each of these quantities is unknown. The index [mass] is given the symbol A, the index of [length], B, and the index of [g], C.

 

In other words

 

[time] = [mass] ^A × [length] ^B × [g] ^C [T] = [M] ^A × [L] ^B × [[L] [T ^–2]]^C

 

(we know that g has the dimension of acceleration [L] [T] ^–2). There are three 'unknowns', A, B, and C, and there are three dimensions, [M], [L], and [T]. [M], [L], and [T] can be equated individually, giving three quite separate equations for the indices of [M], [L], and [T].

 

Equation for [M]

 

0 = A

 

So the mass of the pendulum does not figure in the relationship.

 

Equation for [L]

 

0 = B + C

 

Equation for [T]

 

1 = –2 × C

 

From this equation, C = –½, and it follows from the previous equation that B = +½.

 

So the final relationship is [T] = [M] ⁰ × [L] ^½ × [g] ^½

 

or

 

[time] = [length] ^½ × [g] ^–½.

 

The index ½ means a square root, and the index –½ means dividing by a square root, so

 

[time] = [length]^½ / g ^½
[time] = (l / g)^½

 

The period itself is not, however, equal to (l / g)^½; it is in fact equal to 2π (l / g)^½.

 

The method of dimensions cannot give the pure number, 2π, in the relationship. Only a full derivation from first principles can give this.