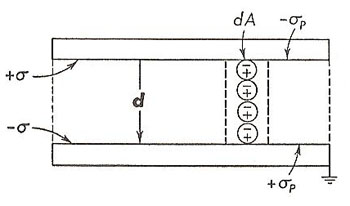
Electric polarization is the extent to which polar molecules have been induced in a dielectric, or in which permanent polar molecules have become aligned under the action of an external electric field. Electric polarization, P, is defined as the electric moment per unit volume. Thus,

 

    P = dp/dv

 

Let us consider, as an example of polarization, the dielectric that is between the plates of a charged parallel-plate capacitor (see diagram). Throughout the body of the dielectric the charges on adjacent ends of polar molecules neutralize one another. At both the upper and lower boundaries of the dielectric, however, ends of polar molecules are exposed. Let the surface density of these exposed charges be σ_P. Consider specifically a tube of the dielectric, of cross-sectional area dA, extending from one capacitor plate to the other. Because the charges at the two ends are - σ_P dA and + σ_P dA, respectively, the dipole moment of this tube of dielectric is

 

    dp = (σ_P dA)d

 

Consequently, in keeping with the definition of polarization,

 

    P = dp/dv = dp/(volume of tube of dielectric) = (σ_P dA)d/(dA)d

 

or

 

    P = σ_P

 

This presupposes, of course, that polarization throughout the dielectric is uniform, in which case the only unneutralized charges are those located at the surfaces of the dielectric. The polarization is then equal in magnitude to the charge per unit area on the surface of the dielectric.

 

For isotropic dielectrics (those whose electrical properties are identical in all directions), the polarization that occurs under the action of an electric field has the same direction as the field. Also, the degree of polarization is a function of the strength of the field. This dependence is expressed as

 

    P = χ_eε₀E

 

where χ_e, the electric susceptibility of the material, is a dimensionless quantity. For most isotropic dielectrics χ_e is constant except for very strong fields.

 

For anisotropic dielectrics, P and E are normally not parallel. Although their relationship is still expressed by the final equation above, the susceptibility is no longer a scalar, as for isotropic materials, but is instead a tensor.