Gravity assist, also known as the slingshot effect, is an important spaceflight technique used successfully on a number of interplanetary missions, including Voyager, Galileo, and Cassini, whereby the gravitational field of a planet is used to increase the speed and alter the course of a spacecraft without the need to expend fuel. The inbound flight path is carefully chosen so that the spacecraft will be whipped around the assisting body, being both accelerated and deflected on a hyperbolic trajectory. At first sight, it may seem as if something has been gained for nothing. However, the additional speed of the spacecraft has been won at the planet's expense which, as a result of the encounter, slows imperceptibly in its orbit and, as a result, moves fractionally closer to the Sun.

 

One of the earliest, and most dramatic applications of the technique came in 1970 when the world watched as NASA used a lunar gravity-assist to rescue the Apollo 13 astronauts after an onboard explosion had severely damaged their spacecraft en route to the Moon. By using a relatively small amount of fuel to put the spacecraft onto a suitable trajectory, NASA engineers and the astronauts were able to use the Moon's gravity to turn the ship around and send it back home.

 

Gravity assist primer

The following description of a gravity assist maneuver comes from the Jet Propulsion Laboratory and applies to the Voyager spacecraft's encounter with Jupiter.

 

From Jupiter's point of view, the situation is similar to a bicyclist speeding up going downhill into a valley, then slowing down again on the uphill part of the road.

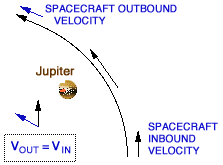
In the vector diagram at the top, the situation is simplified to two dimensions. You can see the magnitude and direction of the spacecraft's velocity on its way in towards Jupiter in the lower diagram. At the upper left, you can see that the accelerating force of Jupiter's gravitation has made a significant change in the direction of the spacecraft's velocity, but not in its magnitude. (These represent velocity at "infinity," from Jupiter, that is, before and after being noticeably changed by Jupiter's presence.) Near the middle of the diagram, the long arrow shows that there's a significant, but temporary, increase in the magnitude (speed). Note these speeds are all with respect to Jupiter.

 

To look at the same phenomenon in terms of a cyclist, V_IN shows the cyclist approaching a downhill grade into a canyon. V_OUT shows that the cyclist slowed down again at the top of the ensuing uphill grade (of course this cycling analogy asks us to ignore air friction and vehicle friction, etc., which are virtually absent in the spacecraft's case). Indeed, after negotiating the canyon, the cyclist's direction has changed, but in the end s/he has not made a lasting change in speed (unless you don't ignore all that friction etc.).

 

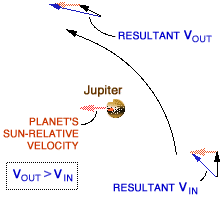
The planet's own motion is a key. A gravity assist with Jupiter involves not a stationary planet as considered above, but a planet with enormous angular momentum as it revolves around the Sun. In the diagram at right, Jupiter's motion along its solar orbit has been illustrated with a vector colored red (simplified, of course: Jupiter revolves along an arc, not a straight line. Imagine the Sun situated below the bottom of the diagram). The spacecraft acquires this Sun-relative vector, or a significant portion of it, during its interaction with Jupiter.

 

You can see how the red vector is added to V_IN and V_OUT. The resulting vector shows how the spacecraft's velocity, relative to the Sun, takes on a nice boost from Jupiter. Notice how rotation of the vector from V_IN to V_OUT (the bending of the spacecraft's path by the planet's gravity) helps increase the result. This trajectory bending is the other key.

 

The spacecraft is a physical mass, so it has its own gravitation. That's how the spacecraft can tug on Jupiter and actually decrease the planet's orbital momentum by a tiny amount. In the exchange, the spacecraft acquires momentum from Jupiter – a significant amount, compared to the momentum the spacecraft already had.

 

History of gravity assist in science and science fiction

Historians of science differ on the issue of when gravity assist as a technique in spaceflight was first discussed in the scientific literature. The mathematics of how cometary orbits are affected by close approaches to planets was known in the late 18th century and in the early 1920s, Walter Hohmann showed that the lowest energy path between any two planets is an ellipse that is tangential to the orbits of both the planets. The first mention of a gravity-assist maneuver may have been by Ray Cummings in his science fiction story "Brigands of the Moon," first published in Astounding in 1931. In this story, an Earth spaceship is piloted by martian brigands who are determined to get their hands on the Moon's one key resource, radiactum ("the catalyst mineral which was revolutionising industry"):

 

We were at this time no more than some sixty-five thousand miles from the moon's surface. The Planetara presently would swing upon her direct course for Mars. There was nothing that would cause passenger comment in this close passing of the moon; normally we used the satellite's attraction to give us additional starting speed.

 

The concept of gravity assist as a means of altering the speed or course of a spacecraft does not appear in scientific literature, however, for another two decades. In a footnote Arthur C. Clarke mentions a paper by Derek Lawden titled "Perturbation Manoeuvres" (Journal of the British Interplanetary Society, vol 13, no 5, Sep 1954). Lawden, a mathematician, worked in the early 1950s on the optimization of rocket trajectories. Somewhat later, in 1961, a summer intern at JPL, Michael A. Minovitch, showed that the gravitational field of a planet could provide thrust to a spacecraft. He demonstrated that careful design of the trajectory to a target planet could provide a gravity assist to move from that planet to another.