Klemplerer rosette
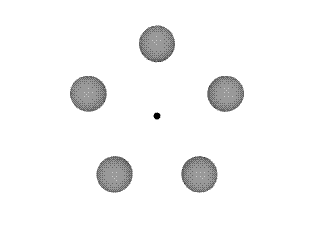
A pentagonal rosette as described in Larry Niven's novel Ringworld.
A Klemplerer rosette is a hypothetical configuration of planets that lack a central star, yet nevertheless orbit a common point. It was first described by W. B. Klemplerer in 1962.1 The concept was brought to widespread attention by the science-fiction writer Larry Niven in his novel Ringworld (1970). In this novel, the use of a Klemplerer rosette (or "Kemplerer rosette" as Niven spells it) is described by a member of the alien species known as Pierson's Puppeteer:
"I had explained," said Nessus, "that our civilization was dying in its own waste heat. Total conversion of energy had rid us of all waste products of civilization, save that one. We had no choice but to move our world outward from its primary."
"Was that not dangerous?"
"Very. There was much madness that year. For that reason it is famous in our history. But we had purchased a reactionless, inertialess drive from the Outsiders. You may have guessed their price. We are still paying in installments. We had moved two agricultural worlds; we had experimented with other, useless worlds of our system using the Outsider drive. In any case, we did it. We moved our world."
"In short, we found that a sun was a liability rather than an asset. We moved our world to a tenth of a light year's distance, keeping the primary only as an anchor. We needed the farming worlds and it would have been dangerous to let our world wander randomly through space. Otherwise we would not have needed a sun at all."
"We had brought suitable worlds from nearby systems, increasing our agricultural worlds to four, and setting them in a Kemplerer Rosette."
Reference
1. Klemplerer, W. B. "Some Properties of Rosette Configurations of Gravitating Bodies in Homographic Equilibrium". Astronomical Journal, vol. 67, number 3, 162–167 (1962).


