Olber's paradox
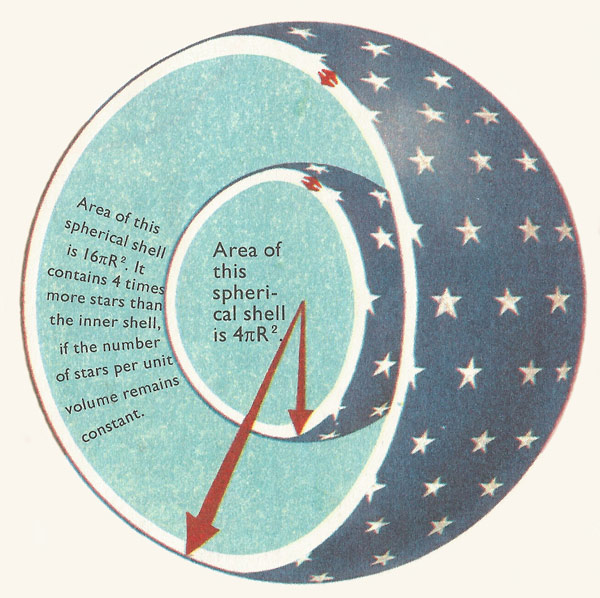
Olbers divided the universe into a series of very thin concentric shells, surrounding the Earth. The illumination on Earth from the shells falls off as the square of the radius. Illumination is proportional to 1/R2. But the illumination also depends on the number of stars in the shell, i.e., it is also proportional to R2. When both are considered, illumination is proportional to R2/R2 = 1. In other words, illumination does not depend on R at all – it is constant. So each shell contributes a certain, constant mount of illumination. An infinite number of shells contribute an infinite amount of illumination.
Olber's paradox is the puzzle of why the night sky is not as uniformly bright as the surface of the Sun if, as used to be assumed, the universe is infinitely large and filled uniformly with stars. It can be traced as far back as Johannes Kepler in 1610, was discussed by Edmond Halley and Philippe Loys de Chéseaux in the eighteenth century, but wasn't popularized as a paradox until Heinrich Olbers took up the issue in the 19th century. It is completely resolved in the standard Big Bang cosmology, according to which the universe has a finite age (providing a horizon beyond which we can't see) and contains a finite number of stars.
Detailed look at the paradox
Is the universe infinite, or does it end somewhere, with completely empty space and nothingness beyond? Olbers argued that if the nearby parts of the universe were a typical sample, repeated again and again in more distant parts, then it would be impossible for the universe to be infinitely large. The universe would contain an infinitely large number of stars and galaxies. Each star radiates light, and no matter how far away the star is, some of its light reaches Earth. The argument continues: if Earth were receiving light from all directions from an infinite number of stars, then the night sky would appear blindingly bright. In every direction there was bound to be a star. The sky would appear to be an unbroken source of light.
In reality, the stars make a very small contribution to the light received on Earth. So according to Olbers, there cannot be an infinite number of them, and the universe must be bounded.
The more distant the star, the smaller the proportion of its light that eventually reaches Earth. The contribution to the illumination on Earth falls off as the square of the star's distance. Quantities that fall off with squares of distances fall off rapidly. Id the Sun were twice as far away, the illumination would be reduced to one quarter. Three times its present distance away, and the illumination would be one ninth, four times away, and the illumination is down to a sixteenth of its present value.
Over large distances, the number of stars in a unit volume is assumed to be fairly constant. Olbers considered the contribution to the illumination on Earth from an imaginary thin spherical shell of stars centered around Earth. The entire universe was divided in this manner into a succession of thin, spherical shells, each one enveloping all the smaller spheres, Olbers calculated the contribution from a typical spherical shell, and then totalled the contributions from all the shells – from the closest immediately surrounding Earth, to the most distant. If the universe were infinite, this outermost shell would be at infinity.
But the paradox was that as the illumination decreased with distance-squared, so the shells became bigger, and contained more stars. In fact, the number of stars in each shell increased as the distance-squared. The increase cancelled out the decrease exactly, and left Olbers with a simple form of summing-up (or integration). If the distance of the most distant spherical shell were infinity, the result of the summing-up would also be infinity. The night sky should appear infinitely bright. Because it is dark, the summing-up cannot be taken as far as infinity Olbers concluded that the universe must be finite.
There are, however, two flaws in his argument that render the conclusion invalid. Much of the matter in space is cold and does not radiate its own light. Interstellar dust, in particular, does not radiate visible light, but absorbs light, and blocks out light from more distant stars. If the interstellar dust were not there, the Earth would receive more light from the stars.
The other flaw came with the discovery that all distant galaxies were receding away from our own Galaxy (this fact is shown by the red shift in their spectra). The more distant they are, the faster their speed or recession; some observed galaxies are receding at close to the speed of light.
The galaxies could stretch out to infinity. None of the light from the most distant ones could ever contribute to the brightness of the night sky.
 |


