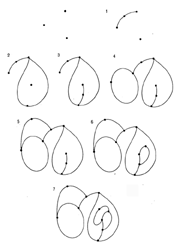
Sprouts is a pencil-and-paper game invented by John Conway and Michael S. Paterson at Cambridge University in 1967. It is played by two players, starting with a few dots (called spots) drawn on a sheet of paper. To make a move, a player draws a curve between two spots or a loop from a spot to itself; the curve may not cross any other curve. The player marks a new spot on the curve, dividing it in two. Each spot can have at most three curves connected to it. The player who makes the last move wins. Sprouts has been studied from the perspectives of graph theory and of topology. It can be proven that a game started with n spots will last at least 2n moves and at most 3n – 1 moves. By enumerating all possible moves, one can show that the first player is guaranteed a win in games involving three, four, or five spots, while the second player can always win a game that start with one, two, or six spots. Following a 1990 computer analysis of the game at Bell Labs out to 11 spots, David Applegate, Guy Jacobsen, and Daniel Sleator conjectured that the first player has a winning strategy when the number of spots divided by six leaves a remainder of three, four, or five.