Thomson effect
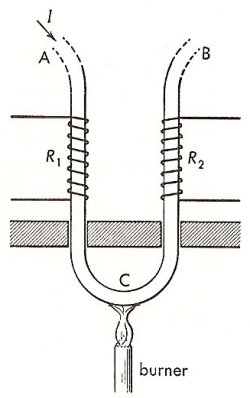
Thomson effect. From Duckworth, Electricity & Magnetism, p 183.
The Thomson effect is one of three reversible thermoelectric phenomena (often known simply as thermoelectric effects), the others being the Seebeck effect and the Peltier effect. In 1851 William Thomson (later Lord Kelvin) was led by thermodynamic reasoning to conclude that sources of electromotive force (emf) exist in a thermoelectric circuit in addition to those located at the junctions. In particular, he predicted that an emf would arise within in a single conductor whenever a temperature gradient was present. The truth of this prediction can be demonstrated by the experiment illustrated in the diagram here.
In this experiment a current passes through an iron rod which is bent into a U-shape. Resistance coils, R1 and R2, are wound about the two sides of the U, as shown. These form two arms of a balanced Wheatstone bridge. The bottom of the U is then heated. This establishes two temperature gradients – a positive one extending from A to C, and a negative one extending from C to B. As a result of this operation, the bridge becomes unbalanced in such a direction as to indicate that the resistance of R1 has increased more than that of R2. Evidently, heat has been liberated at R1 and absorbed at R2.
Absorption of heat is evidence for an electromotive force that is acting in the same direction as that of the current, that is to say, electrical energy is being supplied to the circuit at the expense of heat energy of the environment. Such is the case in the section AB. Likewise, in the section AC, the current is opposed by an emf, with consequent transformation of electrical energy into heat energy. Thus, in iron, the Thomson emf would would give rise to a current in the iron from hot to cold regions. many metals, including bismuth, cobalt, nickel, and platinum, in addition to iron, exhibit this same property, which is referred to as the negative Thomson effect. Another group of metals, including antimony, cadmium, copper, and silver, display a positive Thomson effect; in these, the direction of the Thomson emf is such as to support a current within the metal from cold to hot regions. In one metal, lead, the Thomson effect is zero. In certain metals the effect reverses sign as the temperature is raised or as the crystal structure is altered.
The magnitude of the Thomson emf for a given material, a, is expressed in terms of the Thomson coefficient, σa, which has dimensions of emf/degree. Thus σa dt is the emf that exists between two points whose temperatures differ by dt °C. Hence, the heat absorbed per second between two points at temperature t1 and t2, respectively, when a current of I amperes passes through the material, is given by
Heat absorbed/sec = I [integral between t1 and t2]σa dt – I 2R
The Thomson coefficient, σa, is positive (negative) for materials exhibiting the positive (negative) Thomson effect. The term in the equation above is simply the Joule heat that is always liberated when a current flows through an imperfect conductor. It has no relation to the Thomson effect, but is included in the equation for completeness.
It appears that the total Thomson emf along a conductor depends only upon the temperatures of the two ends, and not in any way upon the particular manner in which the temperature gradient varies. This empirically observed fact is known, after its discoverer, as the law of Malus (1851).


