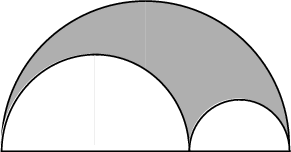
An arbelos is the figure bounded by three semicircles AB, BC, and AC, where ABC is a straight line. Archimedes (about 250 BC) called it an "arbelos" – the Greek word for a knife of the same shape used by shoemakers to cut and trim leather – and wrote about it in his Liber assumptorum (Book of Lemmas).

 

Among the properties of the arbelos are that the sum of the two smaller arc lengths is equal to the larger; the area of the arbelos is π/4 times the product of the two smaller diameters (AB and BC); and the area of the arbelos is equal to the area of a circle whose diameter is the length of a perpendicular segment drawn from the tangent point B of the two smaller semicircles to the point D where it meets the larger semicircle.

 

The circles inscribed on each half of BD of the arbelos (called Archimedes's circles) each have a diameter of (AB)(BC)/(AC). Furthermore, the smallest circumcircle of these two circles has an area equal to that of the arbelos.

 

Pappus of Alexandria wrote on the relations of the chain of circles, C1, C2, C3, ..., (called a Pappus chain or an arbelos train) that are mutually tangent to the two large semicircles and to each other. The centers of these circles lie on an ellipse and the diameter of the nth circle is (1/n) times the base of the perpendicular distance to the base of the semicircle.