atomic structure and the periodic table
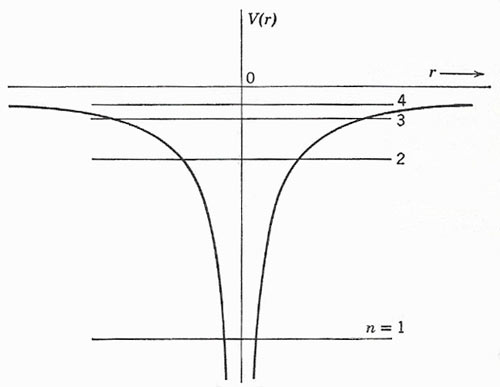
Figure 1. The radial variation of potential, and the first few energy levels, for a hydrogen-like atom.
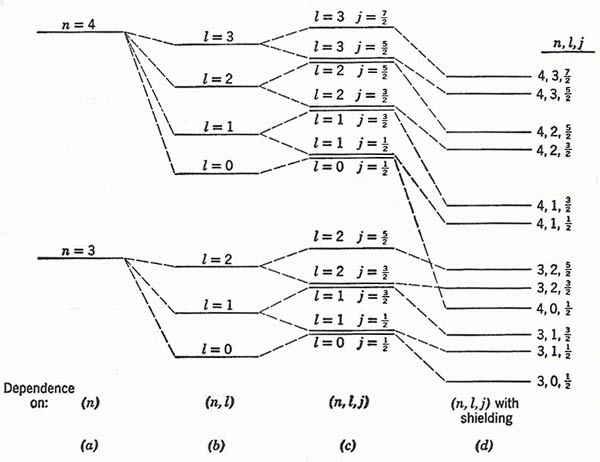
Figure 2. (a) Bohr levels for n = 3 and n = 4. (b) Splitting into levels of different l by Sommerfeld relativistic effect. (c) Doublet splitting of levels of given (n, l). (d) Displacement of levels as a result of shielding. The diagram is purely schematic; no attempt has been made to show anything except the order of the levels, and the energy spacings are quite unrealistic.
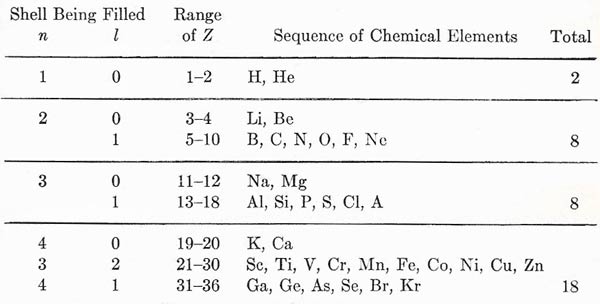
Figure 3. Build-up of the periodic table as electrons are added.
The major consequence of the Pauli exclusion principle (or rather of the property of electron systems that it expresses) is the building up of the electron structure in a many-electron atom. To see how this comes about, let us consider first of all the sequence of levels for one electron moving in the field of a nucleus of charge Ze. The potential energy is given by
so that a section through the origin gives the appearance of a funnel-shaped potential well (Fig 1). The energies of possible states are given to a first approximation by the equation
where C is a constant of the dimensions of energy (actually C = 2π 2me 4/h 2 = 13.5 eV). It is this result that gives special importance to n, the principal quantum number, for it effectively determines the energy of a given state. But, when we consider the problem in more detail, we find that these levels split up into a number of others. It must be remembered that to each value of n there are n different values of l (from zero to n – 1), and to each value of l (except l = 0) there are two values of j. Thus for each n we can expect to find 2n – 1 levels, because
1. Relativistic effects, as calculated by Sommerfeld, cause a separation in energy of the states of different l .
2. The spin-orbit interaction leads to the doublet fine structure for each l (except for l = 0, when j can only be ½.
The scheme of energy levels possible for one electron alone, moving in the Coulomb potential provided by a nucleus, thus becomes very complicated. In the Sommerfeld theory, the most eccentric orbits (i.e. those of the lowest l) lie lowest in energy. We could also argue that, for a given l, the level of smaller j (= l – ½) must lie lower in energy than that for larger j ( = l + ½). For, if we return for a moment to the consideration of doublet structure, we see that the magnetic field H at the position of an electron is in the same direction as the orbital momentum vector L, since L is associated with a circulating positive charge. But the intrinsic magnetic moment μ of the electron is in the opposite direction to the spin momentum S, since in this case we have the circulation of a negative charge.
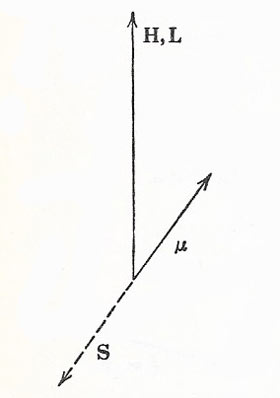 |
| The sign of the spin-orbit interaction makes the magnetic potential energy negative, for a given value of l, when j = l – ½. This case is shown here. |
The magnetic potential energy –μ · H is negative when μ has a positive component along H, but this corresponds to the vector subtraction of S from L, and hence to the smaller value of J. Similarly, when S and L are oriented to give the larger value of J, the magnetic potential energy is positive. When we come to consider a number of elec-rons attached to the same nucleus, the energy level scheme for any one of them is distorted. The principal reason for this is that the presence of other electrons leads to a partial shielding of the electric field due to the nucleus; and we can see, for example, that a nucleus Ze surrounded by (Z – 1) electrons appears from a distance to be electrically identical with a proton. Thus one extra electron, added to make the structure electrically neutral, will behave like the electron in a hydrogen atom so long as it does not penetrate the charge cloud composed of the other electrons. Its potential energy for large r is thus not –Ze 2/r, but something approximating to –e 2/r simply. This will be the case in the kind of circumstances described by a circular orbit of large n according to the old quantum theory (i.e., l = n – 1 in the wave-mechanical description). But, if we take a highly eccentric orbit (i.e. small l) for the same n, the electron can be thought of as penetrating through much of the electron cloud, and experiencing at some point in the orbit almost the full force of the nuclear attraction. This means a greatly enhanced negative contribution to the energy of the electron, so that, in a many-electron atom, the levels of different l are separated very distinctly – much more so, for a given value of n, than the corresponding levels for a single electron.
We can picture the development of the energy level structure in general terms by starting with the Bohr model, and then adding in turn the fine structure due to relativistic change of mass, the doublet structure due to spin, and the distortion due to electron shielding. Fig 2 is a strictly schematic representation for two successive values of the principal quantum number.
Two points of special interest are to be noted:
1. In the Fig 2(c) the levels of the same (n, j) but different l are drawn close together.
2. When electron shielding is taken into account, the levels do all appear as separate. Moreover, the great displacement in energy for penetrating orbits may break down the simple condition that all levels for a given n is should lie lower in energy than all levels belonging to n + 1. In our diagram (d), for example, we show the level for n = 4, l = 0 falling below the two levels for is n = 3, l = 2.
We are now in a position to discuss the building up of the periodic system of the elements. We imagine that we start with the potential well representing the Coulomb field of a nucleus Ze, and that we put into this one electron at a time until we have the full complement of Z electrons. The first electron will certainly fall into the lowest possible state, n = 1, l = 0, j = ½. The second electron can also go into this state, since 2j + 1 = 2 – or in other words we have two distinct orientations of the vector j corresponding to the different values mj = ±½ and this means two recognizably different wave functions, identified by the set of quantum numbers (n, l, j, mj). (In the absence of an external magnetic field the two states have the same energy.) But at this point we have exhausted the possibilities for is n = 1, since by the Pauli principle we can associate only one electron with a given set of quantum numbers. We thus arrive at the concept of what is called a closed shell. This term has a physical significance because the next electron to be added is not so firmly bound to the nucleus as the first two; it has to enter the next higher level (n = 2, l = 0, j = ½), which corresponds classically to a larger radius of orbit (rn ∝ n2) and to a smaller ionization potential In (In = —Enn ∝ 1/n 2). Since j = ½ we can again accommodate two electrons in this level; at this point we again fill a shell and must proceed to is n = 2, l = 1. Here we have two close levels, belonging to j = 1/2 and j = 3/2. The first of these is filled by two electrons, and the second can accommodate four.
The complete development of this structure can now be argued with the help of one or two guiding principles. For given (n, l), the two levels of different j are close in energy, and the distinction between them is not particularly important. We can thus think of a closed shell as consisting of 2(2l + 1) electrons. The closed shell represents a chemically stable structure. The addition of one or two electrons beyond a closed shell gives a looser structure. It is rather easy to detach the extra electrons, leaving a surplus of positive charge in the system as a whole; this is the basis of chemical reactivity and the formation of positive ions, and, in fact, we may expect electronic structures of this type to represent the metals. On the other hand, a structure that is short of a closed shell by one or two electrons will acquire further stability by completing the shell, thereby becoming a negative structure; here we have the possibility of forming negative ions from typical reactive nonmetals such as oxygen and the halogens. The closed shell structure by itself has its obvious expression in the inert gases. By considering the progressive change of Z from 1 up to about 100, we can build up the periodic table in its entirety. We can illustrate the results by taking the first few shells; as shown in Fig 3. The horizontal lines mark the attainment of particularly stable configurations, notably the inert gases He, Ne, A, Kr, etc. We may see the effect of penetrating orbits, with their depressed energies, in the fact that the shell for n = 4, l = 0 lies lower in energy than that for n = 3, l = 2, and so precedes it in the building of the electron system. This corresponds to what we indicated as a possibility in Fig 2. A full analysis of the periodic system in terms of electron quantum states brings to light a large number of finer details, but the present discussion contains most of the underlying features of the problem.


