The Pauli exclusion principle, named after Wolfgang Pauli, states that no two electrons in the same atom can have identical values for all four of their quantum numbers. In other words, (1) no more than two electrons can occupy the same orbital and (2) two electrons in the same orbital must have opposite spins. We'll now look at how this result can be derived mathematically.

 

An important part of wave mechanics is concerned with many-body problems. Let's consider first how we can describe a system of two electrons moving in the same potential. The same set of quantum states will be available to each. We'll denote the wave functions describing these states by ψ_a, ψ_b, etc., and label the electrons as 1 and 2. Then, if one electron is in state a and the other in state b, we can try to set up a single wave function Ψ to describe the whole system, by putting

 

 

The interpretation to be placed on a wave function of this form is that the quantity |Ψ_α|² dτ₁dτ₂, for example, is the probability that electron 1 is in state a and lies within a volume element dτ₁ at r₁, and at the same time electron 2 is in state b and lies within dτ₂ at r₂. Now Ψ_α (or Ψ_β) by itself is not an acceptable wave function, for it carries the implication that a given electron is labeled so that we can tell whether it is definitely in state a or definitely in state b, whereas, if the electrons are truly identical, this distinction is meaningless. We are therefore led to construct a wave function that expresses our ignorance in this matter:

 

 

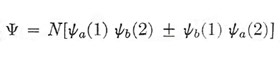If we take the positive sign, Ψ remains unchanged when we imagine an interchange between the two electrons; with the negative sign, Ψ is reversed in sign but retains the same magnitude. Thus in each case Ψ*Ψ, which is the physically meaningful quantity, is unaffected – a condition that will not in general be satisfied for any other form of Ψ. The coefficient N that appears in Ψ, is a normalizing factor. We require

 

 

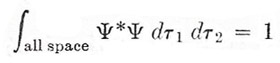This simplifies drastically, because if a and b represent eigenstates of one electron, we have

 

 

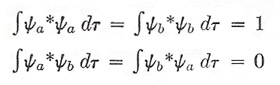which represent the normalization condition (top) and orthogonality condition (bottom).

 

Hence 1 = 2N ², so that N = 1/√2.

 

We therefore arrive at two possible types of wave function for a system of two identical particles:

 

 

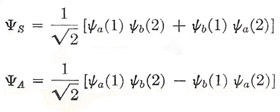The titles "symmetric" and "antisymmetric" are a means of describing what happens to Ψ when the two particles are imagined to be interchanged.

 

Now there is a very obvious property of Ψ_A which proves to be of enormous importance: if we set a = b, i.e., if we suppose our two particles to be in the same quantum state, then Ψ_A vanishes. And this corresponds to a known property of systems of electrons: viz. that, when two electrons are moving in the same field of force (e.g. in the atom), certain states are missing, and they are precisely those states for which the two electrons would have the same set of quantum numbers and so be described by identical wave functions. This discovery was made by Pauli (1925) as a result of a study of spectral data, and was found to be of quite general application to systems of electrons. It has come to be known as the exclusion principle, and can be stated in two equivalent ways:

 

1. No two electrons moving in the same field of force can have the same complete set of quantum numbers (n, l, m_l, m_s) [or the alternative set (n, l, j, m_j)].

2. The wave function describing two electrons is antisymmetric; a symmetric function, though mathematically possible, is never found in nature.

It must be emphasized that the exclusion principle was first put forward as a purely empirical result. A number of years later Pauli (1940) analyzed the problem in a way that suggested an intimate connection between the symmetry of a possible wave function for two identical particles and the magnitude of the particle spin – whether it is an integer or an odd half-integer in units of h/2π.