two-electron systems
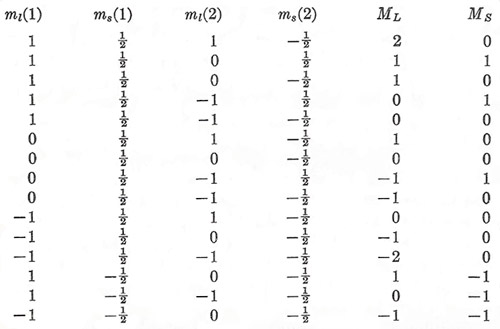
Figure 1. Orbital and spin quantum numbers for a two-electron system.
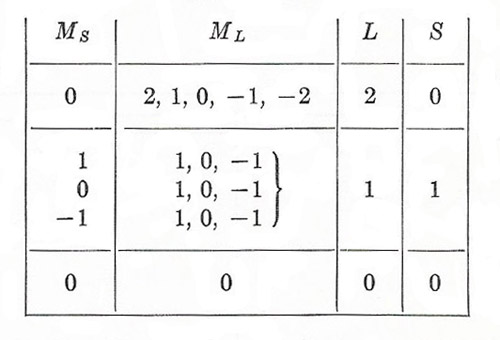
Figure 2. Two-electron combined quantum states.
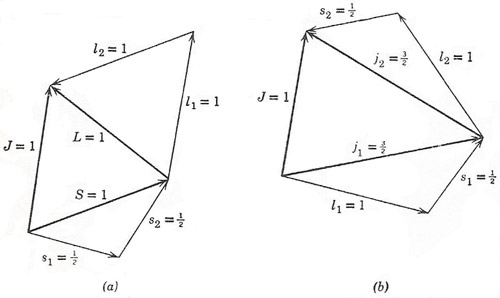
Figure 3. LS and jj coupling for a pair of p electrons (l = 1). (a) L = 1, S = 1, coupling to give J = 1. (b) j1 = 3/2, j2= 3/2, coupling to give J = 1.
To see how the Pauli exclusion principle applies to an actual physical system, let us consider an atom with two electrons in similar states – as for example in the alkaline earth metals, or zinc, or mercury, in which we know from chemistry that there are two valence electrons occupying a special outer position in the atom.
Suppose first of all that both electrons have / = 0 (and the same value of the principal quantum number n). Then each is restricted to the unique value ml = 0 for the z component of l on any specified axis of quantization. Thus the three quantum numbers n, l, ml are the same for both particles, and, according to the exclusion principle, they must differ in the remaining quantum number ms. It follows that one electron must have ms = +½ and the other must have ms = —½. It really is not meaningful to speak of the separate electrons in this way, since they are indistinguishable; what we can do, however, is to give a definite value to the combined values of the orbital and spin momentum components. We designate these as ML, and MS, and so for this case have
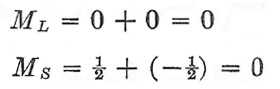 |
No other combinations are possible. Now these M values are what would arise from a combined orbital momentum vector L equal to zero and a combined spin momentum S also equal to zero, and we infer that the separate orbital and spin momentum vectors of the two electrons do indeed combine in this way and in no other. The resultant state is described as a "singlet" state (2S + 1 = 1) having L = 0, and in spectroscopic notation is written as 1S0. As a suffix here we write the value of the total angular momentum J. (J = L + S.)
It should he noted that, if our two electrons did not have the same value of n, the values of ms, would not be restricted to being opposite, but could combine to make MS, equal to +1 or —1 as well as zero. These three possibilities would then correspond to the z components of a combined spin momentum equal to unity, so that, in addition to the state 1S0, we could also have 3S1 (multiplicity = 2S + 1 = 3, J = 1). It was the complete absence of "triplet" states of this sort when n was known to be the same for two s electrons that helped to lead Pauli to the discovery of the exclusion principle.
We have chosen a very simple first application of the Pauli principle; let's now see how it governs the possible states formed by the combination of two equivalent p electrons (l = 1) in the same atom. The problem at once becomes much more complicated, because the value of ml for each electron may assume any of the three values ± 1 or 0. We can solve it, however, by systematically writing down the values of ml and ms for the two electrons so as to exhaust all the different combinations that do not have ml (1) = ml (2) and ms (1) = ms (2) simultaneously (Figure 1). Note that each particular combination (ml , ms)1, (ml , ms)2 appears once only; we do not obtain a new and distinct state by transposing the electrons, because they are indistinguishable.
We see that there are 15 different combined states. A little study shows that they can be classified as shown in Figure 2.
We are thus able to infer that only three distinct types of state are possible:
Singlet D state: 1D2
Triplet P state: 3P0,1,2
Singlet S state: 1S0
The subscripts indicate the values of J that can be formed by the combination of L with S in each case. Notice the conservation of the total number of states – in particular for the P states where we have
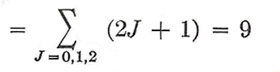 |
A simple way of expressing these results is furnished by the concept of vector addition of angular momenta. For two p electrons, the magnitude of the resultant orbital momentum vector L (= l1 + l2, with l1 = l2 = 1) is restricted to the values 0, 1, 2. The magnitude of the resultant spin S may be 0 or 1. Thus any possible combined state of the two electrons must belong to a singlet or triplet S, P, or D configuration. The detailed applicationof the Pauli principle then limits the allowed combinations of L with S as shown above if both electrons have the same n. This particular way of combining states, based on the (n, l, ml, ms) specification of the individual electron states, is called LS coupling (or Russell-Saunders coupling). We can go through an exactly similar procedure on the basis of the (n,l, j, mj) classification, in which case we have what is called a jj coupling scheme (Figure 3 illustrates the two types of coupling for a pair of p electrons). The choice of which to use is a genuine physical choice; it depends on whether the spin-orbit coupling of an individual electron is broken down or preserved when two electrons interact with each other in orbits of the same n. Usually the LS coupling is the more important for spectroscopy.
The principles outlined here can of course be extended to the case of many electrons, or to the vector combination of angular momenta for electrons having different values of l and j.


