Compton effect
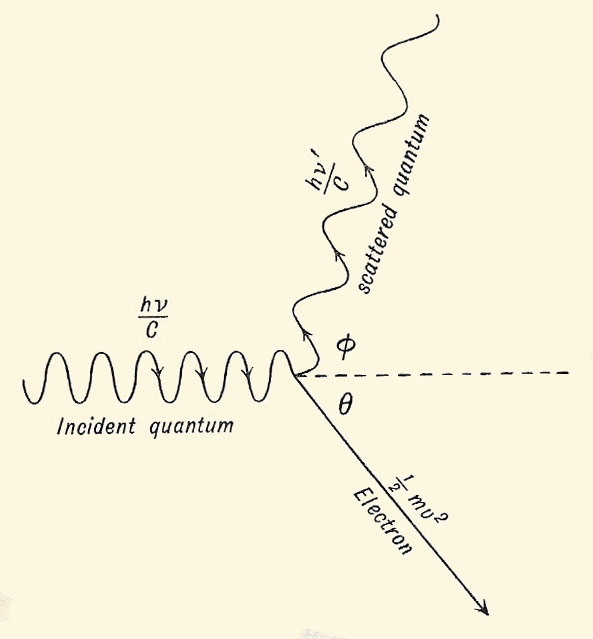
Compton scattering of an X-ray photon by an electron.
X-rays can be scattered by matter in two quite distinct ways. In the first, coherent rays are scattered, without any wavelength change. This type of scattering leads to diffraction effects of which use is made in the crystal grating. The second type of scattering is incoherent, the scattered radiation having a longer wavelength than that of the incident rays. This is called the Compton effect, being first demonstrated and explained by Arthur Compton in 1922.
Compton directed a beam of X-rays on to graphite and measured the wavelength of both the incident radiation and of that scattered in different directions, using a Bragg ionization spectrometer. The scattered radiation was found to consist largely of the incident radiation but associated with this was some radiation with longer wavelength. The change in wavelength was found to depend upon the angle through which the radiation had been scattered.
This effect has been explained by Compton by attributing momentum to the incident quantum of radiation. When such a quantum strikes an electron the latter recoils, absorbing some of the energy of the radiation. The quantum is thus scattered with reduction in energy, leading to an increase in wavelength.
Consider what takes place when a light quantum of energy hν strikes a free electron. Such a quantum can be shown to have a momentum hν/c where c is the velocity of light. As shown in Fig 1, the incident quantum, after striking the electron, is scattered in the direction φ with reduced frequency ν '. The electron moves off with energy mv 2/2 in the direction θ. (Actually the electron mass is m (1 – v 2/c 2)-½ when the effect of increase of mass due to relativity is taken into account. Since the relativity correction cancels in the more exact analysis, it is neglected here.)
From the conservation of energy we have
hν = hν ' + mv 2.
Also, since momentum must be conserved, the forward momentum equation is
hν/c = (hν '/c) cos φ + mv cos θ
And for the transverse components
(hν '/c) sin φ = mv sin θ.
When these equations are solved, the change in frequency ν – ν ' which takes place when the radiation is scattered through an angle φ can be evaluated. Converting wavelengths, if dλ is the wavelength change, it can be shown from the above equations that
dλ = (h/mc)(1 – cos φ).
The numerical value of (h/mc) is 0.024 Å, whence
dλ = 0.024(1 – cos φ) Å.
This shows that the change in wavelength depends upon the angle of scatter φ, the maximum possible change being 0.048 Å. which occurs when φ = 180°. The measurements made by Compton are in complete agreement with the above theory.
It is to be noted that the mass of the recoil particle is involved in the expression for the wavelength shift. The above value has been derived for a free electron. Strictly speaking there will be a Compton effect when any radiation is scattered by any particle. If the latter happens to be an electron bound in an atom its effective mass is considerably increased, with a corres-ponding reduction in the displacement.


