The Császár polyhedron is a polyhedron, first described in 1949 by the Hungarian mathematician Ákos Császár,¹ that is a solution to an interesting problem, namely: How many polyhedra exist such that every pair of vertices is joined by an edge?

 

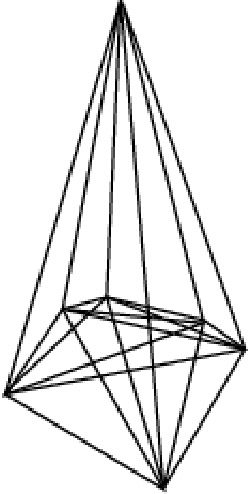
The first clear example is the well known tetrahedron (triangular pyramid). Some simple combinatorics specify how many vertices, edges, faces, and holes such polyhedra must have. It turns out that, other than the tetrahedron, any such polyhedron must have at least one hole. The first possible polyhedron beyond the tetrahedron has exactly one hole; this is the Császár polyhedron, which is thus topologically equivalent to a torus (donut). The Császár polyhedron has 7 vertices, 14 faces, and 21 edges, and is the dual of the Szilassi polyhedron. It isn't known if there are any other polyhedra in which every pair of vertices is joined by an edge. The next possible figure would have 12 faces, 66 edges, 44 vertices, and 6 holes, but this seems an unlikely configuration – as, indeed, to any even greater extent, does any more complex member of this curious family.

 

 

Reference

1. Csaszar, Akos. "A polyhedron without diagonals." Acta Univ Szegendiensis, Acta Scient. Math, 13: 140-142, 1949.