SOLIDS & SURFACES
A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  W  X  Y  Z

                  
  • HOME
  • ABOUT
  • CATEGORIES
  • SITE MAP
  • COPYRIGHT
  • ADVERTISE
  • CONTACT
    •

    entire Web this site



    cone

    cone
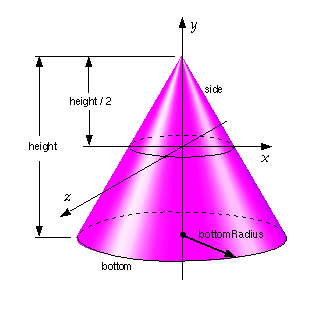
    Dimensions of a cone
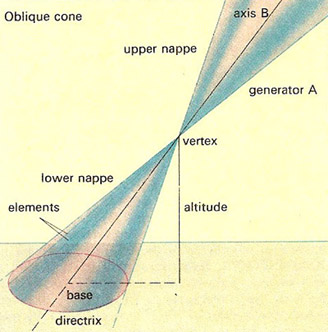
    Terms associated with a cone
    Terms associated with a cone
    A solid geometrical figure (its name comes from the Greek konos for pinecone) that has a circular or elliptical base and a vertex, also known as an apex, lying outside the plane of the base and that is formed from all the line segments joining points on the edge of the base to the vertex.

    If the base is a circle, the shape is a circular cone; if the line, or axis, from the center of the base to the vertex is perpendicular to the base, then it is a right cone (an ice-cream cone is a right circular cone); otherwise it's an oblique cone. The curved lateral surface of the cone is called a nappe. If the cone is extended in both directions from the vertex, the result is a double cone or bicone. A section through a double cone that has been extended indefinitely in both directions to form a conic surface is known as a conic section.

    Another way to think of a cone is as a surface of revolution generated by a line that rotates around a fixed point, at a fixed angle from another line (the axis), both lines passing through that fixed point. The volume of a cone, of perpendicular height h and circular base of radius r, is 1/3πr 2h.

    Take a solid cylinder of radius r and height 2r. Remove the right double cone that passes through the center of the cylinder and extends to meet the circular disks on the cylinder's top and bottom. Interestingly, the volume of the remaining object and the volume of a sphere of radius r are the same.


    Puzzle

    The Cone Puzzle (no. 202) from Henry Dudeney's Amusements in Mathematics1 runs as follows: "I have a wooden cone. How am I to cut out of it the greatest possible cylinder?"

    Solution: The simple rule is that the cone must be cut at one-third of its height.


    Reference
    1. Dudeney, H. E. Amusements in Mathematics. New York: Dover, 1917. Reprinted Mineola, NY: Dover, 1958.

    Related category

       • SOLIDS AND SURFACES





    Also on this site:

    Encyclopedia of Alternative Energy & Sustainable Living
    Encyclopedia of History
    Transport Concepts & Designs (partner site)


    BACK TO TOP