conic sections
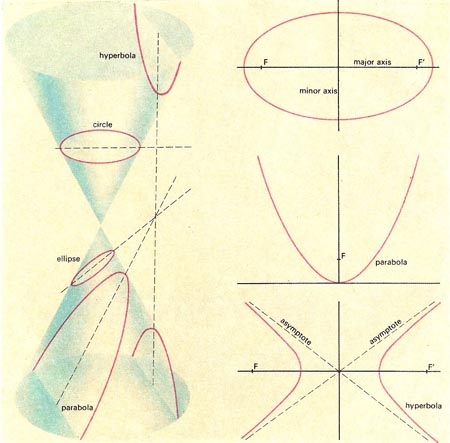
The formation of the conic sections on the surface of a right circular cone and their representation as figures in plane geometry.
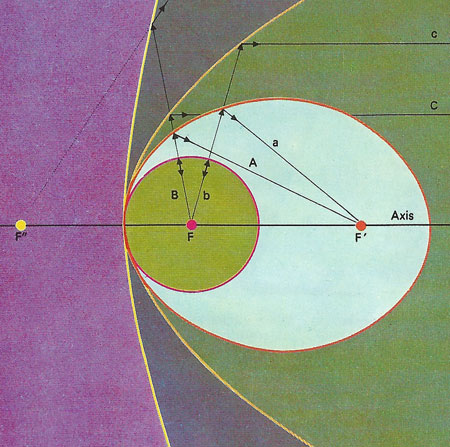
The conic sections all have characteristic reflecting properties. An ellipse has two foci [F, F'] such that rays emitted from one converge [A, a] on the other. A circle is an ellipse with its foci coincident and an emitted ray is reflected straight back [B, b]. A parabola is like an ellipse with the other focus infinitely far away: rays emitted from the true focus are reflected parallel to its true axis [C, c]. The hyperbola reflects rays from F as if they came from another focus F" behind it.
The conic sections are an important, familiar, and ubiquitous family of curves obtained by slicing a right circular double cone, extended indefinitely in both directions, with a plane. Depending on the angle of the slice to the axis of the cone, the resulting curve may be a circle, an ellipse, a parabola, or a hyperbola. The circle is a limiting case of the ellipse, when the slice is made at right angles to the axis, while the parabola is the limiting case of both the ellipse and the hyperbola, when the slice is made parallel to the side of the cone. The name conic sections comes from the eight-volume work Conics by Apollonius, who also gave us the names ellipse, parabola, and hyperbola.
Another geometric way to define the conics is as the locus of all points in the plane whose distances, r, from a fixed point called the focus, and a, from a given straight line called the directrix, have a constant ratio. This ratio, r/a, is known as the eccentricity, e. The circle has an eccentricity of zero. As the eccentricity increases from near zero, corresponding to a nearly-circular ellipse, the ellipse stretches until the right-hand side of it disappears to infinity, e becomes 1, and the ellipse turns into a parabola, with just one open branch. Like the circle, the parabola has only one shape, though it may look different depending on how much it is enlarged or diminished. As the eccentricity increases beyond 1, the "lost" right-hand end of the ellipse reappears from the other side of infinity, so to speak, and turns into the left-hand branch of a hyperbola.
Because a hyperbola is effectively an ellipse split in two by infinity,
it comes as no surprise that these curves are related in an inverse way.
An ellipse consists of all points whose distances from two foci have a constant
sum, while a hyperbola is made from all points whose distances from two
foci have a constant difference. These definitions also apply to the circle
and the parabola, if the two foci are considered to coincide in the case
of the circle and to be separated by an infinite distance in the case of
the parabola.
In terms of algebra, the family of conics represents all the possible real
number solutions to the general quadratic equation ax 2 + bxy + cy 2 + dx + ey + f = 0. In other words, the graph
of any quadratic with real solutions is always a conic section. The key
quantity is the difference b2 – 4ac. If this
is less than zero, the graph is an ellipse, a circle, a point, or no curve.
If b2 – 4ac = 0, the graph is a parabola, two
parallel lines, one line, or no curve; if it is greater than zero, the graph
is a hyperbola or two intersecting lines.
Conic sections also represent all the possible orbits an object can follow when under the gravitational influence of a single massive body.
Directrix
The directrix is the line that, together with a point called the focus, serves to define a conic section as the locus of points whose distance from the focus is proportional to the horizontal distance from the directrix. If the ratio r = 1, the conic is a parabola, if r < 1, it is an ellipse, and if r > 1, it is a hyperbola.
Eccentricity
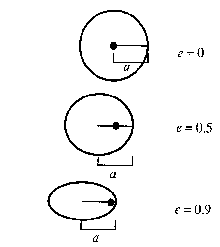 |
Eccentricity is a parameter that describes the shape of an orbit, or any curve that is a conic section. The eccentricity of an ellipse is the ratio of the distance between the foci and the major axis. Equivalently, the eccentricity of an orbit is (ra – rp) / (ra + rp) where ra is the apoapsis distance and rp is the periapsis distance. An almost circular orbit has an eccentricity close to zero. The more elongated the orbit, the higher the eccentricity, up to a maximum value, for a closed orbit, of 1. As a guide, the orbital eccentricity of most of the planets in the Solar System is less than 0.1 (0.017 in the case of Earth), although that of Mercury and Pluto exceeds 0.2. Eccentricity is one of the orbital elements.

