parabola
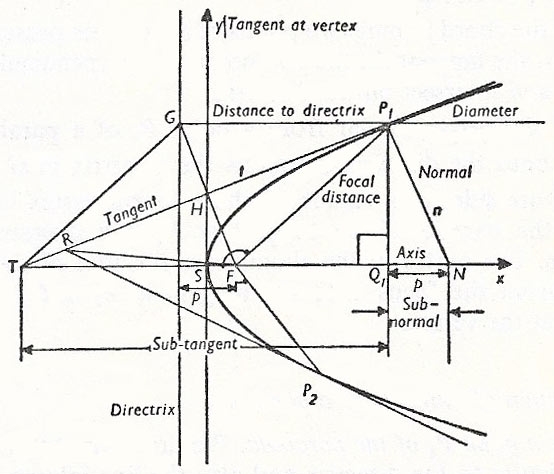
Figure 5. General theorems on the parabola.

Figure 6. The surface of a rotating liquid is a paraboloid.
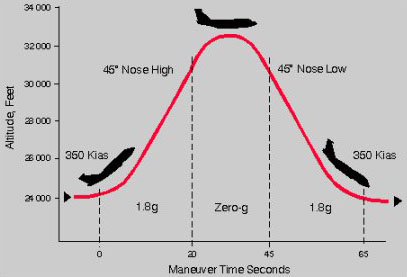
Figure 7. Parabolic flight.
The parabola is a curve, with an eccentricity equal to 1, obtained by slicing a cone with a plane parallel to one side of the cone. It is one of the four types of conic section. A parabola can also be considered to be an ellipse with an infinite major axis.
One of the most studied curves in the history of mathematics, a parabola is the outline of the figure obtained if a right circular cone is cut by a plane that is exactly parallel to the cone's side. Just as the circle is a limiting case of the ellipse when the two foci coincide, the parabola is a limiting case of the ellipse when one of the foci is moved to infinity. As the French mathematician Henri Fabre eloquently put it, a parabola is an ellipse that "seeks in vain for its second, lost center." Johannes Kepler drew this further connection between the parabola and other conic sections:
Because of its intermediate nature the parabola occupies a middle position [between the ellipse and the hyperbola]. As it is produced it does not spread out its arms like the hyperbola but contracts them and brings them nearer to parallel, always encompassing more, yet always striving for less – whereas the hyperbola, the more it encompasses, the more it tries to obtain.
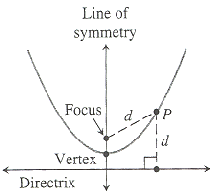 |
| Figure 1. The parabola
|
A parabola is the locus of all points in a plane that are equidistant from a given line, known as the directrix, and a given point not on the line, known as the focus (Fig 1). The Cartesian equation of a parabola that opens upward and has its vertex (turning point) at the origin is y = 4ax 2, where a is the distance from the vertex to the focus, and the quantity 4a is known as the latus rectum. More generally, any quadratic equation of the form y = ax 2 + bx + c, where a is not zero, graphs a parabola. The simplest form of this, when a = 1, and both b and c are zero, is y = x 2. Like the circle, but unlike the ellipse and the hyperbola, the parabola has only one distinct shape. In other words, any parabola can be superimposed exactly on any other parabola simply by rotating, translating (sliding), and/or enlarging or shrinking it.
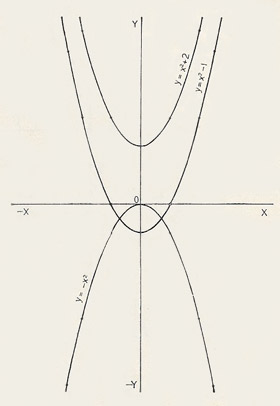 |
| Figure 2. The curve is moved up and down by changing the constant term b in y = ax 2 + b. It is turned upside down by writing –x 2 instead of x 2. But they are all the same curve, only in different positions.
|
Euclid dealt with the parabola in his Conic Sections, and, although this treatise was lost, it provided a foundation for the first four books by Apollonius of the same name. Galileo discovered that a cannonball, or any other projectile launched at an angle to ground, follows a parabolic path: a result that immediately grabbed the attention not only scientists but of monarchs and military leaders. René Descartes, in writing La Géométrie (1637), chose the parabola to illustrate his innovative analytical geometry. In 1992, Rudolph Marcus of the California Institute of Technology won the Nobel Prize in Chemistry for his work showing that parabolic reaction surfaces can be used to calculate how fast electrons travel in molecules. His most famous theoretical result, an inverted rate-energy parabola, predicts electron transfer will slow down at very high reaction free energies.
Particular equations of the parabola
1. Vertex equations
According to the direction of the axis of a parabola, we have the following equations (the vertex of the parabola being taken each times as the origin):
(a) Axis of parabola = y-axis, focus F(0, p/2) (opening above):
x 2 = 2py; directrrix: y = –p/2
(b) Axis of parabola = y-axis, focus F(0, –p/2) (opening below):
x 2 = –2py; directrrix: y = +p/2
(c) Axis of parabola =x-axis, focus F(p/2, 0) (opening to right):
y 2 = 2px; directrrix: x = –p/2
(d) Axis of parabola =x-axis, focus F(–p/2, 0) (opening to left):
y 2 = –2px; directrrix: x = +p/2
If the vertex of the parabola is not taken as the origin of the coordinate system but has coordinatesS(a, b), then the following possibilities arise:
(a) Axis of parabola paralell to y-axis (opening above):
(x – a)2 = 2p(y – b), focus: F(a, b + p/2), directrix: y = b – p/2.
(b) Axis of parabola paralell to y-axis (opening below):
(x – a)2 = –2p(y – b), focus: F(a, b–p/2), directrix: y = b + p/2.
(c) Axis of parabola parallel tox-axis (opening to right);
(y – b)2 = 2p(x – a), focus: F(a+p/2, b), directrix: x = a – p/2.
(d) Axis of parabola parallel tox-axis (opening to left);
(y – b)2 = –2p(x – a), focus: F(a–p/2, b), directrix: x = a + p/2.
2. Equations of lines associated with the parabola
2.1 Intersections
Intersections of the line y = mx + n with the parabola y 2 = 2px.
Regarding the equations: (i) y = mx + n and (ii) y 2 = 2px as a system of equations specifying the points of intersection we have:
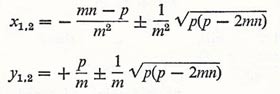 |
Special case: m = 0, the straight line is parallel to the x-axis.
The system of equations is then: y 2 = 2px, y = n. In this case there is only one point of intersection P1 (n 2/(2p), n), and there is no tangent line having this direction.
In the general case we have (D = p – 2mn, the discriminant):
2 points of intersection if D is positive;
1 point of intersection if D = 0 (tangent);
no point of intersection if D is negative.
2.2 Tangents to the parabola
The line y = mx + n is tangent to the parabola y 2 = 2px if D = p – 2mn = 0, i.e. if n = p/2m). The equation of the tangent is then
y = mx + p/(2m).
This line touches the parabola at the point (p/(2m 2), p/m).
The equation of the tangent to the parabola at the point (x1, y1) is yy1 = p(x + x1).
The equation of the normal at the same point is: y – y1 = y1/p (x – x1).
2.3 Polar equations
If the tangents to the parabola from a point P0 outside the parabola are to be constructed and their equations obtained, the points of contact of the required tangents are first calculated by means of the polar equation. This is yy0 = p(x + x0).
2.4 Diameters
Straight lines with a fixed gradient m have equations of the form y = mx + n and form a family of parallel chords of the parabola when n is varied. From the coordinates of the point of intersection we can derive the mid-points of the chords (– (mn – p)/m 2, p/m) and their locus is defined to be a diamter of the parabola. The mid-points of chords of a family with common gradient m therefore lie on a line parallel to the x-axis and at a distance p/m from it. This line is called the diameter with reference to the directon m.
2.5 Tangents to the parabolas y 2 = –2px, x 2 = 2py, x 2 = –2py:
(a) The line y = mx + n is tangent to the parabola y 2 = –2px if D = p + 2mn = 0.
(b) The line y = mx + n is tangent to the parabola x 2 = 2py if D = pm 2 + 2n = 0.
(c) The liney = mx + n is tangent to the parabola x 2 = –2py if D = pm 2 – 2n = 0.
2.6 Equations of a tangent at given point of contact p1(x1, y1) to the parabolas (y – b)2 = ±2p(x – a) or (x – a)2 = ±2p(y – b).
The equations of the tangents are
(y – b)(y1 – b) = p.(x – a + x1 – a) for the parabola (y – b)2 = 2p(x – a).
(y – b)(y1 – b) = –p.(x – a + x1 – a) for the parabola (y – b)2 = –2p(x – a).
(x – a)(x1 – a) = p.(y – b + y1 – b) for the parabola (x – a)2 = 2p(y – b).
(x – a)(x1 – a) = –p.(y – b + y1 – b) for the parabola (x – a)2 = –2p(y – b).
2.7 Equations of polar for given pole P0(x0, y0) in respect of the parabolas (y – b) 2 = ±2p(y – b)
The equation of the polar line is identical with the equation of a tangent (see section 2.6) and is obtained by substituting the coordinates (x0, y0) for (x1, y1) in the equation. The polar equation can be used to calculate the point of contact of tangents from P0 to the parabola, and from these to set up the equations of the tangents.
General theorems of the parabola
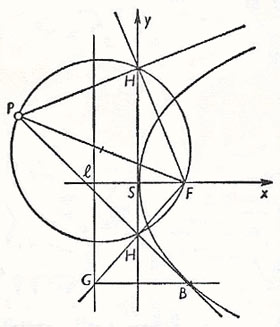
Refer to Figure 5.
1. Diameters of a parabola (with reference to families of parallel chords) are parallel to the axis of the parabola.
2. The feet of perpendiculars from the focus to tangents to a parabola lie on the tangent at the vertex.
3. The point of intersection of two mutually perpendicular tangents lies on the directric of the parabola.
4. The distance of the point of contact of a tangent from the focus is equal to the distance of the focus from the point of intersection of the tangent with the axis of the parabola. (In Fig 5, T F = FP1.)
5. The tangent at P, bisects the angle between P1F and the perpendicular from P1 onto the directrix.
6. The projection onto the axis of the parabola of the line-segment between the point of contact of a tangent and the point of intersection of the tangent with the axis is bisected by the vertex. The segment bisected is referred to as the subtangent.
7. The projection onto the axis of the parabola of the segment lying on the normal, between its points of intersection with the parabola and with the axis, is called the subnormal. The sub-normal has length p.
8. The mirror-image of the focus, with respect to a tangent, lies on the directrix of the parabola.
9. If the tangents at points P1, P2 of a parabola intersect in R, then RFP1 = RFP2.
10. If the chord joining two points of a parabola passes through the focus, the tangents at the two points are perpendicular to one another and intersect on the directrix.
11. If the perpendicular from a point P1 of a parabola with focus F onto the directrix intersects the directrix in G then P1F and P1G are sides of a rhombus whose fourth vertex lies on the axis of the parabola. The tangent at P1 is a diagonal of the rhombus. The center of the rhombus is the foot of the perpendicular from the focus onto the tangent at P1 and lies on the tangent at the vertex.
Construction of tangents to a parabola
 |
|
|
(a) At a point P, of the parabola. We draw through P, the line perpendicular to the directrix and also the line joining P1 to the focus. The tangent is the bisector of the angle between these two lines. (b) From a point P to the parabola. Join the point P to the focus F and describe on the segment PF the Thales circle. The point of intersection of this circle with the tangent at the vertex is the foot H of the perpendicular from the focus onto the required tangent. Join FH and let it intersect the directric in G. G is the mirror-image of the focus with respect to the required tangent. Through Gdraw the line parallel to the axis of the parabola. This intersects the tangent in its point B of contact with the parabola.
Dürer's shell curve
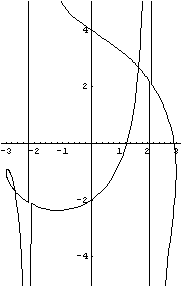 |
| Figure 3. Dürer's shell curve
|
Dürer's shell curve may be defined as follows: given a parabola and a line that is tangent to the parabola, it is the glissette of a point on a line sliding between the parabola and the tangent. It has the equation
(x 2 + xy + ax - b 2) = (b 2–x 2)(x–y + a) 2.
Paraboloid
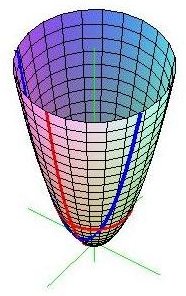 |
| Figure 4. The paraboloid
|
A paraboloid is the surface of revolution of a parabola (Fig 4). It is a quadratic surface described by the equation z = a(x 2 + y 2).
A uniformly rotating liquid acquires a paraboloidal surface (Fig 6) from the interaction of gravity and centrifugal forces, as can be seen by spinning a pan of liquid on a turntable. This surface is perfect for radio- and optical-telescope mirrors; a mirror surface can be made by spinning plastic resin in a dish while it sets and coating it with a metal.
Parabolic flight
A parabolic flight (Figure 7) is the following of a special parabolic trajectory by a suitably fitted airplane in order to reproduce the conditions of weightlessness for a short period. Such flights are used as a routine part of astronaut training.
On the upward arc, the thrust of the airplane is adjusted so that there is no lift: the plane is in free fall since nothing reduces the force of gravity. The plane remains in free fall over the top of the parabola and part of the downward arc. Microgravity conditions are achieved for time periods of 15 to 25 sec.
The four-engine Boeing KC-135, similar to the commercial Boeing 707 aircraft, has been modified by NASA to support parabolic flights. The parabolas are performed in a restricted zone, about 8,000 and 12,000 meters in altitude.
Parabolic velocity
Parabolic velocity is the velocity which an object at a given point would require in order to describe a parabola about the center of attraction. This is also the escape velocity since it is the upper limit of velocity on a closed curve. It is obtained by multiplying the velocity of an object moving in a circular orbit by the square root of 2 (approx. 1.414). For example, if Earth's mean velocity around the Sun of 29.8 kilometers per second. (18.5 miles per second), in a near circular orbit, were increased to 42 kilometers per second (26 miles per second), Earth would move to a parabolic path and escape from the Solar System.

