ellipse

Figure 1. The ellipse is one of the family of curves known as conic sections, the others being the circle, parabola, and hyperbola.
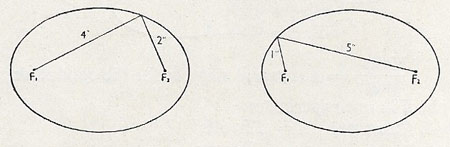
Figure 2. The sum of the distances of any point on the ellipse from the two foci is constant. This law is used in drawing ellipses, as shown below.

Figure 3. An ellipse, such as that followed by a planet in orbit around the Sun, can be easily drawn by using a pencil, a loop of string, and two nails in a board.
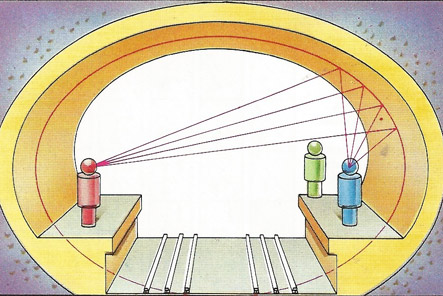
Figure 4. Paris Metro tunnels are almost elliptical and whispering on one platform can be heard on the other by the focusing effect.
An ellipse is a type of conic section mathematically defined (i) by passing a plane through a right circular cylinder at an angle greater than 0 and less than 45 degrees (Figure 1), or (ii) as the locus of a point which moves so that the sum of its distances from two fixed points, known as foci (singular: focus), is constant (Figure 2). If the two foci coincide then the ellipse is a circle. The ellipse is symmetric with respect to both its axes, and is a closed curve.
The line passing through the foci is called the major axis of the ellipse; half this is the semi-major axis, a. The line passing through the center of the ellipse (the midpoint of the foci) at right angles to the major axis is called the minor axis, half of which is the semi-minor axis, b. The focal radius is a line segment from the focus of an ellipse to a point on the perimeter of the ellipse.
An ellipse centered at the origin of an x-y coordinate system with its major axis along the x-axis is defined by the equation
x 2/a 2 + y 2/b 2 = 1
The shape of an ellipse is expressed by a number called the eccentricity, e, which is related to a and b by the formula b 2 = a 2(1 – e 2). The eccentricity is a positive number less than 1, or 0 in the case of a circle. The greater the eccentricity, the larger the ratio of a to b, and therefore the more elongated the ellipse. The distance between the foci is 2ae.
The area enclosed by an ellipse is πab. The circumference of an ellipse is 4aE(e), where the function E is the complete elliptical integral of the second kind.
Elliptical orbits
The closed path followed by one object that is gravitationally bound to another – for example, by one of the stars in a binary star system or Earth as it goes around the Sun (Figure 3). That the orbits of the planets are ellipses, not circles, was first established by Johannes Kepler based on the careful observations of Tycho Brahe.
Semi-major axis
The semimajor axis is half the longest distance across an ellipse. The semimajor axis is one of the orbital elements – a standard parameter used to describe an elliptical orbit. The semimajor axis is also the average distance of an orbiting object from its primary. The periapsis and apoapsis distances, rp and ra, can be calculated from the semimajor axis, a, and the eccentricity, e, by the formula
rp = a(1 – e) and ra = a(1 + e)
 |
| semimajor axis
|
Oval
An oval is a curve that looks like a squashed circle but, in contrast with the ellipse, doesn't have a precise mathematical definition. The word oval comes from the Latin ovus for "egg." Unlike ellipses, ovals sometimes have only a single axis of reflection symmetry (instead of two).
Ellipsoid
 |
| Figure 5. An ellipsoid (in fact, an oblate spheroid).
|
An ellipsoid is a quadratic surface that is the three-dimensional analog of an ellipse. The general equation of an ellipsoid in Cartesian coordinates is
x 2/a 2 + y 2/b 2 + z 2/c 2 = 1
where a, b and c are positive real numbers determining the shape. If two of these numbers are equal, the ellipsoid is a spheroid (Figure 5); if all three are equal, it is a sphere. The intersection of an ellipsoid with a plane is a single point or an ellipse. Ellipsoids can also be defined in higher dimensions.
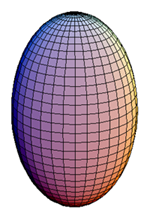
Spheroid
 |
| Figure 6. Prolate spheroid.
|
A spheroid is a surface in three dimensions obtained by rotating an ellipse about one of its principal axes. If the ellipse is rotated about its major axis, the surface is called a prolate spheroid, similar to the shape of a rugby ball (Fig 6). If the minor axis is chosen, the surface is called an oblate spheroid (similar to the shape of the Earth). The sphere is a special case of the spheroid in which the generating ellipse is a circle. A spheroid is a special case of an ellipsoid where two of the three major axes are equal.

