velocity
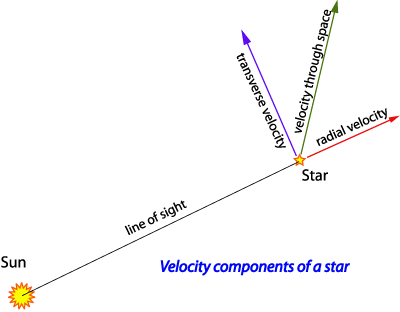
Figure 1. Radial and transverse components of a star's velocity.
Velocity is a vector quantity specifying both the speed and direction of movement of an object in a given frame of reference. The magnitude of velocity is the scalar quantity speed (S), related to distance (s) and time (t ) by the equation S = s/t; similarly velocity (v) is related to distance and time by v = ds/dt. Angular or rotational velocity is given by ω = dθ/dt.
angular velocity
Angular velocity is the rate at which a rotating object sweeps out an angle relative to a fixed point. Angular velocity may be measured in radians, degrees, or revolutions per unit time.
The average angular velocity ω of an object moving from angle θ1 to θ2 in time t, is (θ1 – θ2)/t. Instantaneous angular veolcity is the value approached by ω as t tends to zero. The direction associated with the angular velocity of an object is perpendicular to the plane of its motion. The speed v of an object at a distance r from a fixed point is directly proportional to the magnitude ω of its angular velocity: v = rω.
escape velocity
The escape velocity is the minimum velocity that a less massive object, such as a rocket, runaway star, or rogue planet, must have in order to escape completely from the gravitational influence of another, more massive body, such as a planet or a star, without being given any extra impetus. It can be calculated by taking the square root of (2Gm /r) where r is the distance from the center of the gravitating body of mass m, and G is the gravitational constant. This is equal, but in the opposite direction to the velocity it would have acquired if it had been accelerated from rest, starting an infinite distance away. The escape velocity can also be thought of as the velocity an object needs in order to attain a parabolic orbit – the lowest-energy open orbit. For an object leaving Earth's surface this is 11.2 kilometers per second( about 7 mlie per second). An escape orbit is any orbit whose apoapsis lies at infinity. This includes parabolic orbits, followed objects with parabolic velocity, and hyperbolic orbits, followed by objects with hyperbolic velocity. If the body's velocity is less than the escape velocity, it is said to be gravitationally bound.
| planet | escape velocity (km/s) |
| Mercury | 3.20 |
| Venus | 10.08 |
| Earth | 11.12 |
| Mars | 4.96 |
| Jupiter | 59.20 |
| Saturn | 35.20 |
| Uranus | 20.80 |
| Neptune | 24.00 |
| Pluto | 1.1 |
orbital velocity
The orbital velocity is the velocity of an object at a given point in its orbit. If the orbit is perfectly circular, the magnitude of the velocity is constant and given by
Vorb = √[G(M + m)/r ],
where G is the gravitational constant, M is the mass of the primary gravitating body, m is the mass of the orbiting object, and r is the radius of the orbit. In this special case, orbital velocity is the same as circular velocity.
If the m is negligible compared with M, as it is, for example, in the case of a spacecraft orbiting Earth, then this equation reduces to
Vorb = √(GM /r ).
An object moving faster than circular velocity will enter an elliptical orbit with a velocity at any point determined by Kepler's laws of planetary motion. If the object moves faster still, it will travel at escape velocity along a parabolic orbit or beyond escape velocity in a hyperbolic orbit.
radial velocity
The radial velocity is the speed at which an object is moving away from or toward an observer along the line of sight (Figure 1). By convention, it is positive if receding, negative if approaching.
In the case of luminous astronomical objects, radial velocity can be calculated from the displacement of spectral lines from their normal position: a object moving toward us has a blueshifted spectrum, while an object moving away has a redshifted spectrum. The larger the blueshift or redshift, the larger the radial velocity. The present radial-velocity champion for a star in the Milky Way Galaxy is Giclas 233–27 in Lacerta, which is approaching us at 583 kilometers per second. External galaxies and, especially, quasars, may show very large recessional radial velocities due to the overall expansion of the universe. Compare with transverse velocity.
terminal velocity
Terminal velocity is the constant velocity finally attained by a body moving through a fluid under gravity when there is no resultant force acting on it. It is dependent on the shape of the body and the resistance of the air through which it is moving. See also viscosity.
Terminal velocity is also the hypothetical maximum speed that a body, under given conditions of weight and thrust, could attain along a specified straight flight path, if diving though an unlimited distance in air of uniform density.
transverse velocity
Transverse velocity is the component of the velocity of an object, such as a star, that is at right-angles to the observer's line of sight; also known as tangential velocity (Figure 1). To calculate a star's transverse velocity, the star's distance and proper motion must be known. If the transverse velocity and radial velocity are known, it is a simple matter to calculate the object's velocity through space.


