Fifteen puzzle
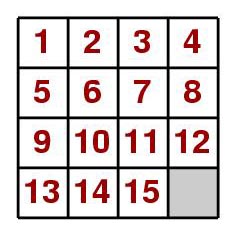
A sliding-tile puzzle, which Sam Loyd claimed
to have invented in the 1870s (but see below), that became a worldwide obsession,
much as Rubik's cube did a century later.
Fifteen little tiles, numbered 1 to 15, were placed in a four by four frame
in serial order except for tiles 14 and 15, which were swapped around; the
lower right-hand square was left empty. The object of the puzzle was to
get all the tiles in the correct order; the only allowed moves were sliding
counters into the empty square. Everyone it seemed was caught up with the
craze – playing the game in horse-drawn trams, during their lunch
breaks, or when they were supposed to be working. The game even made its
way into the solemn halls of the German parliament."'I can still visualize
quite clearly the gray-haired people in the Reichstag intent on a square
small box in their hands," recalled the geographer and mathematician Sigmund
Gunter who was a deputy during the puzzle epidemic. "In Paris the puzzle
flourished in the open air, in the boulevards, and proliferated speedily
from the capital all over the provinces," wrote a contemporary French author.
"There was hardly one country cottage where this spider hadn't made its
nest lying in wait for a victim to flounder in its web." Loyd offered a
$1,000 reward for the first correct solution. But, although many claimed
it, none were able to reproduce a winning series of moves under close scrutiny.
There is a simple reason for this, which is also the reason that Loyd was
unable to obtain a U.S. patent for his invention. According to regulations,
Loyd had to submit a working model so that a prototype batch could be manufactured
from it. Having shown the game to a patent official, he was asked if it
were solvable. "No," he replied. "It's mathematically impossible." Upon
which the official reasoned there could be no working model and thus no
patent!
The puzzle's theory reveals that the more than 20 billion possible starting
arrangements of the tiles fall into just two groups: one in which all the
tiles can be maneuvered into ascending numerical order (call this group
I), and one in which tiles 14 and 15 will be inverted (group II). It's impossible
to combine arrangements from these two groups and impossible to turn a group
I arrangement into a group II, or vice versa, using the normal rules of
the game. Given a random arrangement of tiles, can we know in advance if
we have one of the unsolvable kind? Very easily. Simply count how many instances
there are of a tile numbered n appearing after the tile numbered n + 1.
If there are an even number of such inversions, the puzzle is solvable,
otherwise you are wasting your time!
Although Sam Lloyd claimed to have invented the Fifteen puzzle, he had,
in fact, nothing to do with promoting or popularizing it. The actual inventor
was Noyes Chapman, the Postmaster of Canastota, New York, and he applied
for a patent in March 1880. This and other surprising details are described
in a book called The 15 Puzzle, by Jerry Slocum and Dic Sonneveld.1
Reference
- Slocum, Jerry and Dic Sonneveld. The 15 Puzzle. Slocum Puzzle
Foundation: 2006.
Related entry
• mechanical
puzzles
Related categories
• GAMES
AND PUZZLES
Also on this site:
Encyclopedia
of Alternative Energy & Sustainable Living
Encyclopedia
of History
BACK TO TOP
|
