geodesy
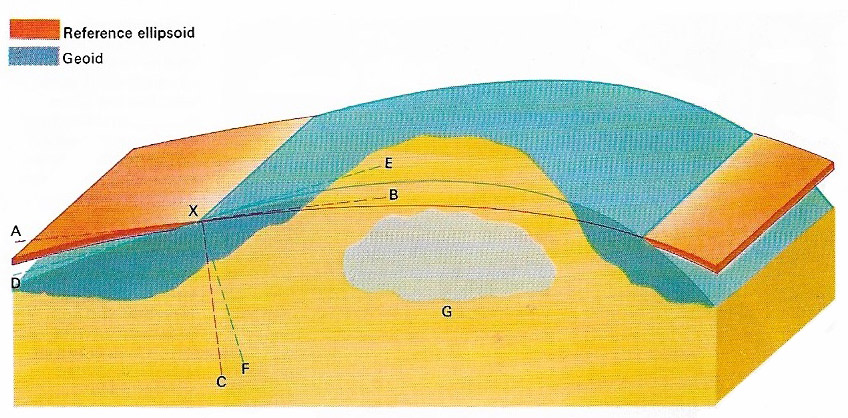
Figure 1.

Figure 2. Equipment used for a geodetic survey. Photo by John Galetzka, US Geological Survey.
Geodesy is the science of determining the size and shape of Earth and the precise location of points on its surface. The first recorded measurement of the Earth's circumference that approximates to the correct value was that of Eratosthenes in the 3rd century BC. Modern geodesists use not only the techniques of surveying but also information received from the observations of geodesy satellites.
Earth's rotation creates a centrifugal force that is greater at the equator than elsewhere, causing the Earth to bulge out slightly at the equator and to flatten at the poles. This makes the Earth diameter at the equator greater than that through the poles by about 41 km (25 miles).
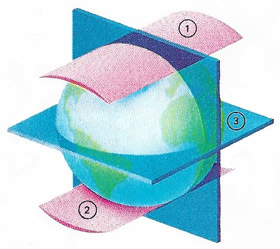 |
| The Earth's surface is not a true sphere but approximates to an ellipsoid whose equatorial diameter exceeds its polar diameter. The difference is about 41 kilometers (25 miles) and may be illustrated by forcing hypothetical wedges (1, 2) through the spaces over the poles; this would not be possible at the equator (3). This equatorial bulge is caused by the effect of centrifugal force as the Earth rotates on its axis. |
Mean sea-level is the average sea-level between tides and is taken as the base level when measuring altitudes. It is always perpendicular to the force of gravity. Such a surface, taken all over Earth is known as the geoid, which is what Earth's true shape is called. The surface of the geoid is irregular because the gravity field varies locally and depends on the type of rocks in the crust. A large ore body or mountain chain will deflect a nearby plumbline away from the center of Earth and thus the geoid's shape is obtained by directly measuring gravity on land or its varation at sea, where wave motion precludes direct measurement. Perturbations of artificial satellite orbits are now extensively used for broad-scale geoid studies. The shape of the geoid is defined by its departure from a "reference ellipsoid" which fits most closely to the shape of Earth; in this case, the average level of the land and sea is taken as the norm. Mountains are then higher and sea-floors lower than the surface of this ellipsoid. (An ellipsoid is the regular geometric shape obtained by revolving an ellipse round one of its axes.)


