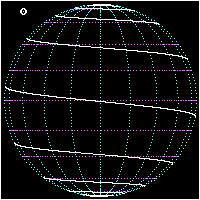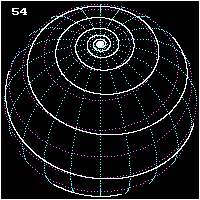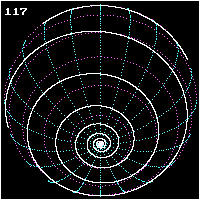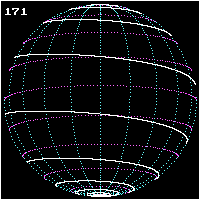
A loxodrome is a path on Earth's surface that is followed when a compass is kept pointing in the same direction. It is a straight line on a Mercator projection of the globe precisely because such a projection is designed to have the property that all paths along the Earth's surface that preserve the same directional bearing appear as straight lines.

 

The loxodrome isn't the shortest distance between two points on a sphere. The shortest distance is an arc of a great circle. But, in the past, it was hard for a ship's navigator to follow a great circle because this required constant changes of compass heading. The solution was to follow a loxodrome (from the Greek loxos for slanted and drome for course), also known as a rhumb line, by navigating along a constant direction. In middle latitudes, at least, this didn't lengthen the journey unduly.

 

If a loxodrome is continued indefinitely around a sphere it will produce a spherical spiral, or a logarithmic spiral on a polar projection. The loxodrome can be written in terms of the longitude and latitude of a point on the curve and its angle with the meridians; there is no advantage in using parametric equations.

 

History of the loxodrome

The loxodrome was discovered by the Portuguese mathematician and geographer Pedro Nuñez after observations reported to him in 1533 by Admiral Martim Alfonso de Sousa. In 1569 the Flemish cartographer Geradus Mercator designed a world map with cylindrical projection such that the meridians and parallels were straight lines, intersecting at right angles, and whose distance from each other increased with their distance from the equator. The Mercator projection distorts the image (especially at high latitudes) but has the great advantage of showing loxodromes as straight lines; such maps are still important tools for navigation at sea and in the air.