Malfatti circles

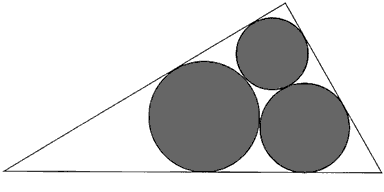
In 1803 the Italian mathematician Giovanni Malfatti (1731–1807) posed the following problem: Given a triangle, find three non-overlapping circles inside it such that the sum of their areas is maximal. Malfatti and many other mathematicians thought that the solution is given by the three circles each of which is tangent to the other two and also to two sides of the triangle. Malfatti computed the radii of these circles, and they are now known as Malfatti's circles.

Later it became clear that the conjecture of Malfatti is not true. In particular, Goldberg proved in 1969 that the Malfatti circles never give a solution of the Malfatti problem! In other words, for any triangle there are three nonintersecting circles inside it, whose areas are bigger than the area of the Malfatti circles. So far as is known, the Malfatti problem hasn't been solved yet in the general case although it seems reasonable to conjecture that the solution is given by what is called the greedy algorithm: We first inscribe a circle in the given triangle; then we inscribe a circle in the smallest angle of the triangle which is tangent to the first circle. The third circle is inscribed either in the same angle or in the middle angle of the triangle, depending on which of them has the bigger area.

Related category

• PLANE CURVES

Also on this site:

Encyclopedia of Alternative Energy & Sustainable Living
Encyclopedia of History

BACK TO TOP