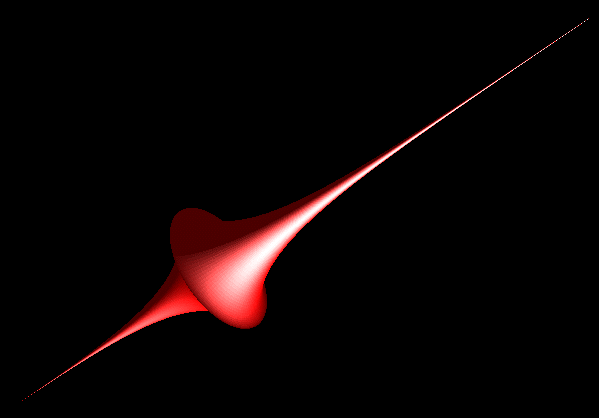
A pseudosphere is a saddle-shaped surface that is produced by rotating a tractrix about its asymptote. The name "pseudosphere," which means "false sphere," is misleading because it suggests something that is sphere-like; however, a pseudosphere is almost exactly the opposite of a sphere. Whereas a sphere has a constant positive curvature (equal to +1/r, where r is the radius) at every point on its surface, a pseudosphere has a constant negative curvature (equal to –1/r) everywhere. As a result, a sphere has a closed surface and a finite area, while a pseudosphere has an open surface and an infinite area. In fact, although both the two-dimensional plane and a pseudosphere are infinite, the pseudosphere manages to have more room! One way to think of this is that a pseudosphere is more intensely infinite then the plane. Another result of the pseudosphere's negative curvature is that the angles of a triangle drawn on its surface add up to less than 180°.

The geometry on the surfaces of both the sphere and the pseudosphere is a two-dimensional non-Euclidean geometry – spherical (or elliptical) geometry in the case of the sphere and hyperbolic geometry in the case of the pseudosphere. Astronomers currently suspect that the universe we live in may have a hyperbolic geometry and thus have properties analogous to those of a pseudosphere.