Curvature is a measure of the amount by which a curve, a surface, or any other manifold deviates from a straight line, a plane, or a hyperplane (the multidimensional equivalent of a plane). For a plane curve, the curvature at a given point has a magnitude equal to one over the radius of an osculating circle (a circle that "kisses," or just touches, the curve at the given point) and is a vector pointing in the direction of that circle's center. The smaller the radius r of the osculating circle, the greater the magnitude of the curvature (1/r) will be. A straight line has zero curvature everywhere; a circle of radius r has a curvature of magnitude 1/r everywhere.

 

Another way to define the curvature at any point P on a plane curve is the difference between the angle θ made by the tangent at that point with a fixed straight line, and the angle θ + δθ made by the tangent at the adjacent point P' with the same straight line. The curvature at P may therefore be defined as the rate of change, k, or θ at that point. In terms of differential calculus, for the curve y = f (x)

 

 

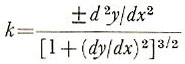Types of curvature

For a two-dimensional surface, there are two kinds of curvature: a Gaussian curvature (or scalar curvature) and a mean curvature. To compute these at a given point, consider the intersection of the surface with a plane containing a fixed normal vector (an arrow sticking out perpendicularly) at the point. This intersection is a plane and has a curvature; if the plane is varied, this curvature also changes, and there are two extreme values – the maximal and the minimal curvature, which are known as the main curvatures, 1/R₁ and 1/R₂. (By convention, a curvature is taken to be positive if its vector points in the same direction as the surface's chosen normal, otherwise it is negative.) The Gaussian curvature is equal to the product 1/R₁R₂. It is everywhere positive for a sphere, everywhere negative for a hyperboloid and pseudosphere, and everywhere zero for a plane. It determines whether a surface has elliptic (when it is positive) or hyperbolic (when it is negative) geometry at a point. The integral of the Gaussian curvature over the whole surface is closely related to the surface's Euler characteristic. The mean curvature is equal to the sum of the main curvatures, 1/R₁ + 1/R₂. A minimal surface, like that of a soap film, has a mean curvature of zero.

 

Curvature tensor

In the case of higher-dimensional manifolds, curvature is defined in terms of a curvature tensor, which describes what happens to a vector that is transported around a small loop of the manifold.

 

The curvature tensor is the basic mathematical object in Einstein's general theory of relativity. It determines how the tipping of light cones changes from time to time and place to place in the history of the universe.

 

Curvature constant

The curvature constant is a constant (k) appearing in the Robertson-Walker metric which determines the curvature of the spatial geometry of the universe. The three standard Friedmann models have: k > 0 for positive curvature (spherical geometry), k < 0 for negative curvature (hyperbolic geometry), and k = 0 for zero curvature (flat geometry).