tractrix
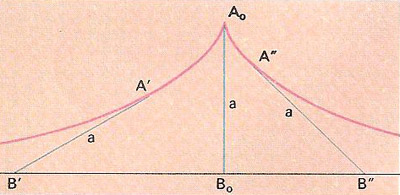
Part of the tractrix (locus of A) for the line AB of length a.
The tractrix is a curve, sometimes called the trajectory curve or equitangential curve, to which a straight line AB, of length a, is always a tangent at A as B moves along the x-axis from –∞ to +∞. The term is sometimes loosely used to describe the solid formed by rotation of the curve about the x-axis.
The tractrix is the answer to a question asked by the Frenchman Claude Perrault (1613–1688). Perrault is not a giant in the annals of mathematics; in fact, he trained as a doctor and gained a minor reputation as an architect and an anatomist before dying in unusual style as a result of an infection he caught while dissecting a camel. His greatest claim to fame, aside from his connection with the tractrix, is that he was the brother of the author of "Cinderella" and "Puss-in-Boots." In 1676, at about the time Gottfried Leibniz was doing groundbreaking work on the calculus, Perrault placed his pocket-watch on the middle of a table, pulled the end of its chain along the edge of the table, and asked: What is the shape of the curve traced by the watch?
The first known solution was given in a letter to a friend in 1693 by Christiaan Huygens, who also coined the name "tractrix" from the Latin tractus for something that is pulled along. (The corresponding German name is hundkurve, or "hound curve," which makes sense if you imagine the path a dog might follow on its leash as its master walks away.) The tractrix can also be found by taking the involute of a catenary. (Imagine a horizontal bar held at the vertex of the catenary and the point of contact marked as P. When the bar is rolled against the catenary without slipping, the path of P is a tractrix.) It is described by the parametric equations: x = 1/cosh(t ), y = t – tanh(t ).
The surface of revolution of the tractrix is the pseudosphere, which is the classic model for hyperbolic geometry and one possible three-dimensional analog for the shape of the four-dimensional spacetime in which we live.

