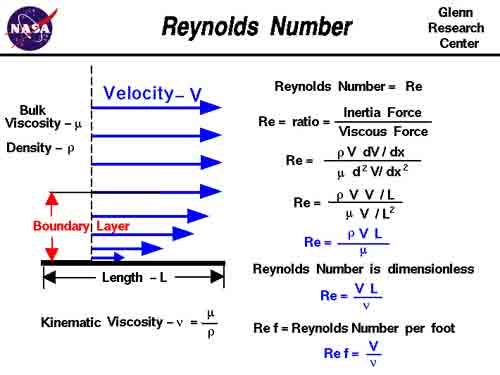
Reynolds Number (Re) is the most important dimensionless number in fluid dynamics. It is the ratio of inertial forces to viscous forces and is given by the formula:

 

    Re = ρVD / μ

 

where ρ = density of the fluid, V = velocity, D = pipe diameter, and μ = fluid viscosity.

 

Reynolds Number is used to determine whether a flow will be laminar or turbulent. If Re is high (> 2100), inertial forces dominate viscous forces and the flow is turbulent; if Re is low (< 1100), viscous forces dominate and the flow is laminar. It is named after the British physicist and engineer Osborne Reynolds (1842–1912), of the University of Manchester, who discovered it in 1883.

 

Reynolds Number is important in wind tunnel experiments since it relates to the aerodynamic properties of lifting surfaces, such as airfoils, when extrapolating from small wind tunnel test models to full-size wings. Reynolds discovered that, if the same atmospheric pressure were used for experiments with wind tunnel models as a full-size aircraft would encounter under actual conditions, the experimental results would be invalid.

 

In order for results obtained with a scale model in wind tunnel experiments to be valid, the Reynolds Number needs to be the same under wind tunnel conditions and in regular atmospheric conditions. The way to ensure this is to increase the air density inside the tunnel by the same proportion as the model is smaller than the full-size aircraft. In practical terms, if a model is 1/10 the size of a full-size aircraft, then the air density (the number of atmospheres) inside the tunnel must be increased by a factor of 10 to get wind tunnel results that are valid in regular atmospheric conditions with a full-size aircraft.

 

Reynolds discovered the ratio that has since been called the Reynolds Number when examining fluid flow characteristics – how a liquid flows in a pipe or how air flows across an aircraft wing. He demonstrated that the motion of a fluid may be either laminar (in smooth layers) or turbulent, and that the change from a laminar flow to a turbulent flow can happen suddenly. The transition from a smooth laminar flow to a turbulent flow always occurred when the ratio ρVD / μ was the same (ρ = density of the fluid, V = velocity, D = pipe diameter, μ = fluid viscosity. The variable that can be adjusted inside a wind tunnel is ρ – its density, and it would be adjusted by the same proportion as the model is smaller than the actual aircraft: a 1/10th model would produce valid results if the atmospheric pressure in the wind tunnel were increased by a factor of 10.

 

In actual subsonic flight, airfoils with low Reynolds Number flows are laminar and those with high Reynolds Number flows are mostly turbulent, keeping in mind that the Reynolds Number is the ratio between density, velocity, diameter, and viscosity (For an airfoil in flight rather than in a wind tunnel, D would be the distance between the leading and trailing edge called the chord length along a flow.)