volume
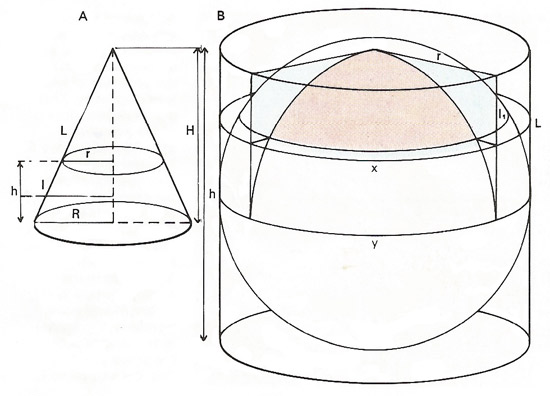
Volumes and areas of solid figures.
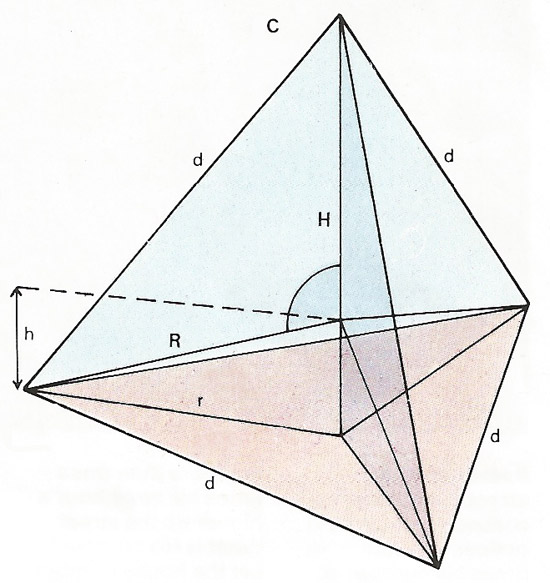
Regular tetrahedron.
Volume is the measure of space occupied by a three-dimensional body.
The volumes and areas of solid figures can be linked by formulas. In a cone [A] the volume of the full cone is 1/3πR 2H; and the area of the curved surface is given as πLR. In the frustrum of the cone (lower section) the area of the curved surface = πl(R + r); and the volume = 1/3πh(R 2 + Rr + r 2).
In a sphere and cylinder [B], the surface area of the sphere = 4πr 2. The curved surface of the cylinder = 2πrh.The volume of the sphere = 4/3πr 3; and of a cylinder it is π r 2h. The volume of the section of sphere between planes x and y = Vs = π [L2(r – L/3) – l12(r – l1/3)]. In a regular tetrahedron [C] the distance r = d /√3; H = d (√2/√3); and r = 1/2d (√3/√2). The height of the center of gravity is given as h = H /4.
Scaling
If the size of a balloon is doubled, its surface (and therefore weight) goes up four times, but its volume (and therefore lift) goes up eight times/ This surface/volume scaling law shows that balloons become more efficient the gigger they are. Conversely, doubling an aircraft's size increases its weight by eight times, but the wing area by ony four times. Small aircraft pose fewer design problems.
 |


