differential geometry
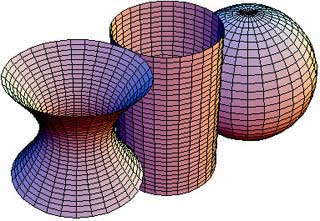
Surfaces of constant Gaussian curvature.
Differential geometry is the study of geometry using calculus; it has many applications in physics, especially in the general theory of relativity. The objects studied by differential geometry are known as Riemannian manifolds (see manifold). These are geometrical objects, such as surfaces, that locally look like Euclidean space and therefore allow the definition of analytical concepts such as tangent vectors and tangent space, differentiability, and vector and tensor fields. Riemannian manifolds have a metric, which opens the door to measurement because it allows distances and angles to be evaluated locally and concepts such as geodesics, curvature, and torsion to be defined.


