Archimedean spiral
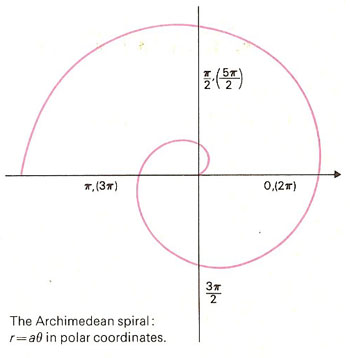
Archimedean spiral.
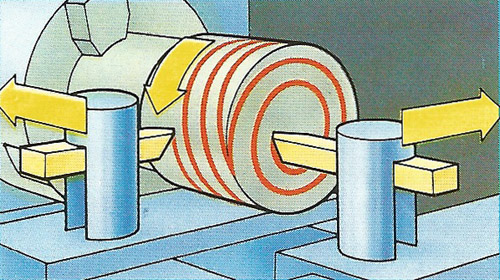
An Archimedean spiral is traced by a point that travels around a center, varying in distance from it in proportion to the angle it moves through. Similarly a helix is the curve of a point that moves around a cylinder, tracing along it in proportion to its total angular rotation. Both are created automatically by a lathe whose cutting tool traverses a rotating work piece. Many cylindrical objects show their machine finishing as a fine helical path.
An Archimedean spiral is a spiral, like that of the groove in a phonograph record, in which the distance between adjacent coils, measured radially out from the center, is constant. It was first studied by Archimedes and was the main subject of his treatise On Spirals. The Archimedean spiral has a very simple equation in polar coordinates (r, θ):
r = a + bθ
where a and b can be any real numbers. Changing the parameter a turns the spiral, while b controls the distance between
the arms.
The Archimedean spiral is distinguished from the logarithmic spiral by the fact that successive arms have a fixed distance (equal to 2πb if θ is measured in radians), whereas in a logarithmic spiral these distances form a geometric sequence.
Note that the Archimedean spiral has two possible arms that coil in opposite directions, one for θ > 0 and the other for θ < 0. Many examples of spirals in the man-made world, such as a watch spring or the end of a rolled carpet, are either Archimedean spirals or another curve that is very much like it – the circle involute.


