Archimedes' principle
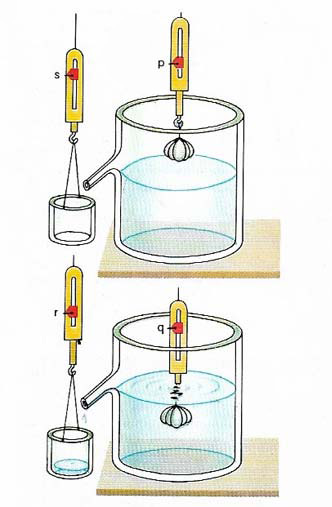
Archimedes' principle states that for an object immersed in a fluid the upthrust on it equals the weight of fluid that its volume displaces. The round object suspended on the balance has weight p in air and lesser weight q when immersed in a liquid. The difference in its weight is equal to the upthrust on it in the liquid; that is, to the weight of displaced water in the beaker, which equals r minus s and which in turn equals p minus q.
Both liquids and gases are fluids and each is able to exert or transmit a force. If a cork is pushed below a liquid surface and then released, it immediately bobs to the surface. The cork has experienced an upward force, called the upthrust, due to the liquid, and it is this that keeps the cork floating on the surface. In exactly the same way, an upthrust must act on a floating balloon, although here it is produced by a gas rather than a liquid.
It was the Greek scientist Archimedes (287–212 BC) who first quantified this fact by stating that "when an object is totally or partially immersed in a fluid the upthrust on it is equal to the weight of fluid displaced". He supposedly formulated this principle after stepping into a bath and watching it overflow. According to legend, he became so excited that he ran out into the street naked shouting "Eureka! Eureka" ("I've found it! I've found it!").
Using Archimedes' principle (1) the magnitude of the upthrust can always be found and it makes itself apparent as a loss of weight of the object.
For this reason, a floating object has its weight exactly balanced by the upthrust. But if the object is too dense, the upthrust may not be sufficient to counterbalance its weight and the object sinks. This principle of flotation is used directly by a hydrometer, an instrument for measuring liquid densities. A hydrometer floats at a level that depends on the weight of a liquid it displaces and, since the submerged volume is known, the density of the liquid can be calculated.


