 |
|
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
| • HOME • ABOUT • CATEGORIES • USE OF TEXT AND IMAGES • NEWSLETTER   
|
Avogadro constant
 |
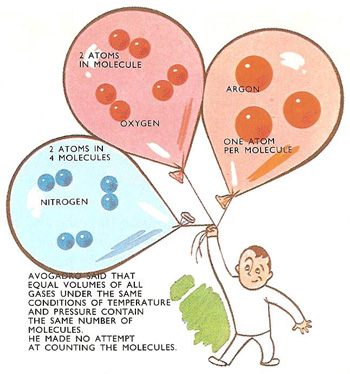
| Avogadro's hypothesis explained
|
Dealing with tiny particles and large numbers
There's no difficulty in counting how many peas there are in a packet, because peas are fairly large and it's easy to pick up a handful and count them one by one. Peas are easy to count; so are particles a thousand times smaller. When they are too small to be seen with the eye alone, they can be counted under a microscope. Some particles, however, are too small and numerous to be dealt with this way.Avogadro's constant is the number of molecules in one mole (or, in older terminology, one gram-molecule) of any substance. This number has the same value for all elements and compounds. There are 6.025 × 1023 molecules, for example, in every 32 grams of oxygen and in 18 grams of steam or water or a gram molecular weight of any other substance. (32, 2, and 18 are the molecular weights of oxygen, hydrogen, and water.)
How the number was discovered and measured
Amedeo Avogadro died in 1856, but the first attempts at finding the actual value of Avogadro's number – it only later became known as Avogadro's constant – were not made until nine years after his death. The work on finding this figure was done by the Austrian physicist Johann Josef Loschmidt.Avogadro had started the train of thought by suggesting that matter might be made up of molecules, tiny invisible clusters of atoms. Containers each of the same size filled with gases, all at the same temperature and pressure, would contain the same number of molecules. When Loschmidt discovered a way of counting the molecules on a gram-molecule, the answer was called, by scientists in other countries, Avogadro's number in honor of the Italian. In Austria and Germany, though, the number was known as Loschmidt's number.
Loschmidt had a difficult problem to solve – that of counting an enormous number of particles that were far too small for him to see. His result was not the result of experiment, but largely that of reasoning. He assumed that the molecules in a gas were in total chaos, bouncing and rebounding all over the place with all sorts of different speeds. To this situation he applied statistical reasoning. This reasoning gave only very rough results, because he overlooked certain factors. Later results of finding Avogadro's constant are much easier to understand and give much better results because they are based on the results of experiments.
 |
Related entry
• Perrin, Jean Baptiste (1870–1942)Related categories
• PHYSICAL CHEMISTRY• NOTABLE NUMBERS
Also on this site:
Encyclopedia of Alternative Energy & Sustainable Living
Encyclopedia of History