Boolean algebra
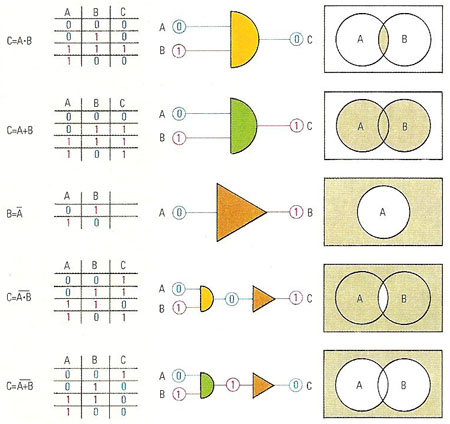
Five basic logic statements are illustrated here. In any of them, if A is true then the table will show a "1", if A is false there will be a "0". In the statement AND, C is true (i.e. there is a "1" in the truth table) when A and B are true, but it is false if either A or B is false. With OR, C is true if either A or B is true and it is only false if both A and B are false. NOT has one input and one output, its function is to reverse "true" and "false"; when applied to AND and OR, their inverses, NAND and NOR, result. The Boolean statements shown here are also illustrated by symbolic circuit elements (inputs on the left and outputs on the right) and by Venn diagrams as in set theory (the outcome is shown by the shaded areas.
1. Boolean algebra is based on the principles of mathematical logic developed by the nineteenth century mathematician George Boole. It is the study of operations carried out on variables that can have only one of two possible values (see binary); i.e., 1 (true) and 0 (false). As ADD, SUBTRACT, MULTIPLY, and DIVIDE are the primary operations of arithmetic, AND, OR, and NOT are the primary operations of Boolean logic. In the Pascal programming language a boolean variable is a variable that can have one of two possible values, true or false. See also logical operation.
2. In another sense, Boolean algebra is an algebra in which the binary operations are chosen to model the union and intersection operations in set theory. For any set A, the subsets of A form a Boolean algebra under the operations of union, intersection, and complement.


