algebra
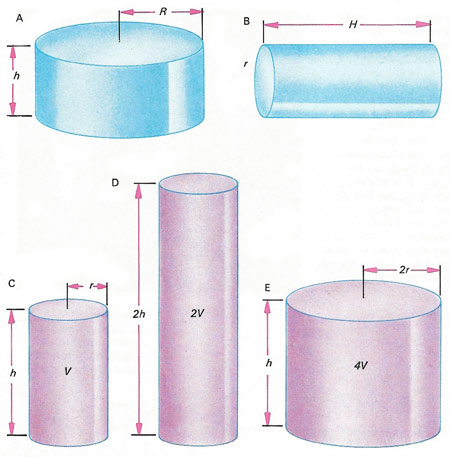
Figure 1. The formula for finding the volume of a cylinder is V = πr 2h, where r is the radius of one end and h is the height. The two cylinders [A and B] have the same volume, but very different radii and heights. In fact, the diameter of one is almost equal to the height of the other, that is h is about equal to 2r and 2R is almost the same as H. Another cylinder [C] has volume V. Doubling its height doubles its volume [D] (for C volume = πr 2h, for D vol. = 2πr 2h). But doubling the radius of the cylinder increases its volume four-fold [E] (for E volume is equal to π(2r)2h = 4πr 2h). These changes are predicted using algebra.
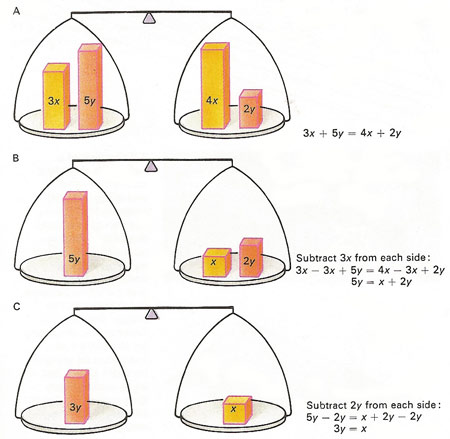
An equation in algebra is in a state of balance; the terms on the left-hand side taken together equal those on the right-hand side, just as a collection of objects balances on a pair of scales [A]. In simplifying an equation it is essential that the same operation be carried out on each side. For example, 3x is subtracted from each pan of the balance [B] (and from each side of the equation). A further simplification is made [C] by subtracting 2y from each side. As a result the original equation 3x + 5y = 4x + 2y reduces to 3y = x. It is also possible to multiply or divide each side by a factor.
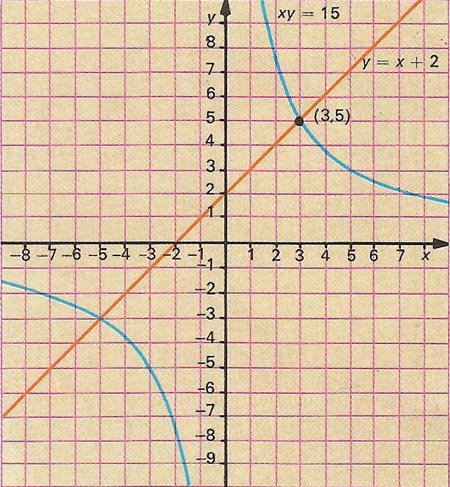
Figure 2. Algebraic equations can be plotted as lines on a graph, a technique that is the province of analytical geometry. This graph shows plots of the equations xy = 15 and y = x + 2. Treated as simultaneous equations, they are both true at the points where the lines cross. When the equation to a straight line is expressed in the form y = mx + c, where m and c are constants, the letter m is a measure of the slope of the line, here equal to 1.
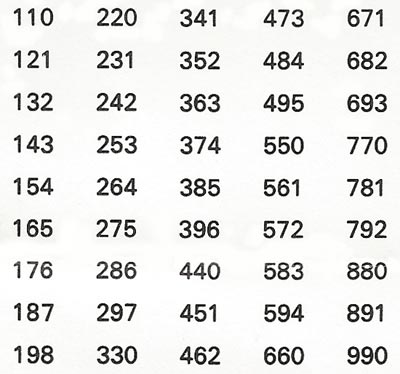
Figure 3. The three-digit numbers in this table have two properties in common: the middle digit is the sum of the other two and all of them are divisible by 11. If the first digit is x and the third y, the middle one is (x + y). The whole number has the value 100x + 10(x + y) + y. This expression can be factorized and simplified to 11(10x + y); it is a general formula for all the numbers in the table and 11 as a factor.
Algebra is a major branch of mathematics that, at an elementary level, involves applying the rules of arithmetic to numbers, and to letters that stand for unknown numbers, with the main aim of solving equations. Beyond the algebra learned in high school is the much vaster and more profound subject of abstract algebra.
The word itself comes from al-jebr, which is Arabic for "the reunion of broken parts;" it first appeared in the title of a book, Al-jebr w'al-mugabalah, by the 9th century Persian scholar, Abu Ja'far Ben Musa, also known as al-Khowarizmi – probably the greatest mathematician of his age, and as famous among Arabs as Euclid and Aristotle are to the Western World.
History of algebra
The oldest work in the West on algebra is that of Diophantus of Alexandria, in the 4th century AD. It consisted originally of 13 books, and contained arithmetical problems; only six books are now extant. The modern Europeans got their first acquaintance with algebra, not directly from the Greeks, but, like most other knowledge, from the Arabs, who derived it, in turn, from the Hindus. The chief European source was the work of Mohammed Ben Musa, who lived in the time of Calif Al Maman (812–833); it was translated into English by Rosen (1831). An Italian merchant Leonardo Boccio, of Pisa, traveling in the East about 1200, acquired a knowledge of the science, and introduced it among his countrymen upon his return; he left a manuscript work on algebra.
The first work on algebra after the revival of learning is that of the Minorite friar Paciolo or Luca Borgo (Venice, 1494). Scipio Ferreo in Bologna discovered, in 1505, the solution of one case of cubic equations. Tartaglia of Brescia carried cubic equations still further, and passed on his discoveries to Girolamo Cardano of Milan as a secret. Cardano extended the discovery himself and published, in 1545, the solution known as "Cardano's rule." Ludovico Ferrari and Bombelli (1572) gave the solution of biquadratic equations.
Algebra was first cultivated in Germany by Christian Rudolf, in a work printed in 1524; Stifel followed with his Arithmetica Integra (1544). Robert Recorde in England, and Pelletier in France, wrote in about 1550. Vieta a Frenchman (d. 1603), first made the grand step of using letters to denote the known quantities as well as the unknown. Harriot, in England (1631), and Girard, in Holland (1629) still further improved on the advances made by Vieta.
The Géométrie of Descartes introduced a major new approach in algebra. It applied geometry to algebra, and was the first to represent the nature of curves by means of equations. Fermat also contributed to the science; and so did the Arithmetica Universalis of Newton.
Algebraic equations and formulae
Common practical applications of algebraic equations are the various formulae used in science, particularly in mathematics and physics. The volume of a cylinder, for example, is given by the formula V = πr 2h, where V is the volume, r is the radius of one end, and h is the cylinder's height (Figure 1). The formula provides a shorthand way of saying "the volume of a cylinder equals the area of one end multiplied by the height".
Algebraic equations and formulae can be manipulated according to established rules. The subject (V) of the cylinder equation can be changed to find the radius or height of a cylinder of known volume. For instance, h = V/πr 2. Such formulae are perfectly general – they apply to all cylinders, whether they are tall and thin or short and squat. There are similar formulae for the areas and volumes of all common geometrical figures.
Many problems in algebra involve more than one unknown quantity. Consider the problem of finding two positive numbers whose product is 15 and whose difference is 2. Let the two numbers be represented by the letters x and y. Then the "product" information can be stated as the equation xy = 15. There are several possible solutions to this equation: 1 and 15, 3 and 5, 7.5 and 2, and so on. To proceed we must use the "difference" information, which generates the equation y – x = 2, rearranging to give y = x + 2. Substituting this expression for y in the first equation yields x(x + 2) = 15, or x 2 + 2x – 15 = 0.
Now this third equation contains only one unknown quantity: x. The only positive number that satisfies it is 3 (when the equation becomes 9 + 6 – 15 = 0). Finally, to find y we substitute this value of x in either of the two original equations. According to the first, y = 15/x = 15/3 = 5 and for the second y = x + 2 = 3 + 2 = 5. The answer to the problem is therefore 3 and 5. In algebraic terms, we have solved two equations that are both true at the same time – called simultaneous equations.
By considering points in space defined by referring to their distances from a line (the x-axis) and another line (the y-axis), the equations of algebra take on a whole new meaning. The equation xy = 15, for example, represents a curve on which all points have the product of their x-distance and y-distance equal to 15. The equation y = x + 2 represents a straight line and all points along it satisfy this equation.
If these two curves are drawn (to a mathematician, even a straight line is a 'curve'), they intersect at the point whose x-distance is 3 and whose y-distance is 5 – the point defined as (3, 5). The graphs approach to the problem gives exactly the same solution as the purely algebraic approach. It also reveal another point at which the curves intersect, corresponding to x = –3 and y = –5. These solutions are, however, disallowed by the original problem, which called for two positive numbers (Figure 2).
The whole procedure of plotting algebraic equations as curves is the province of analytic geometry – the branch of mathematics in which algebra and geometry come together.
Algebra also supplies an insight into other puzzles and paradoxes. Any three-digit number whose middle digit is the sum of the other two is divisible by 11. Why? The answer can be supplied using algebra (Figure 3).
Algebraic operation
An algebraic operation is an operation of ordinary algebra; that is, any of the arithmetic operations of addition, subtraction, multiplication, and division. Operations that involve infinite series and functions such as log x are not algebraic – they depend on the use of limits. The term algebraic is also applied to arithmetic operations carried out with due regard to sign. Thus, the algebraic sum of a and –b is a – b, the algebraic product of –a and –b is +ab, etc.
Algebraic function
An algebraic function is a function that may be expressed in a finite number of terms, involving only the elementary algebraic operations of addition, subtraction, multiplication, division, and root extraction. For instance,
f (x) = πx 3 + x¼ – 2/x
is an algebraic function. They are distinguished from transcendental functions, such as the exponential, logarithmic, and trigonometric functions, which can be expressed only by an infinite series.
Another way of saying this is that the function f (x) is algebraic if y = f (x) is a solution of an equation of the form pn(x)y n + ... + p1(x)y + p0(x) = 0 where the p0(x), p1(x), ... , pn(x) are polynomials in x. All polynomials are algebraic. A function that satisfies no such equation is transcendental.
There are various types of algebraic function. A rational function is one in which there are no fractional powers of the variable or variables. Integral functions do not include the operation of division in any of their terms. A homogeneous function is one in which the terms are all of the same degree – i.e., the sum of the indices of the variables in each term is the same for every term. For example, u 4 + u 3v + u 2v 2 + uv 3 + v 4 is a rational, integral, homogeneous function of the fourth degree in u and v.
Fundamental theorem of algebra
The fundamental theorem of algebra is the result that every algebraic equation of the nth degree
a0 x n + a1x n–1 + ... + an–1x + an = 0
whose coefficients are real numbers possesses at least one real or complex root. An algebraic equation of the nth degree with one unknown, and real coefficients, possesses exactly n roots, provided every solution (real and complex) is counted according to its multiplicity.



