multiplication
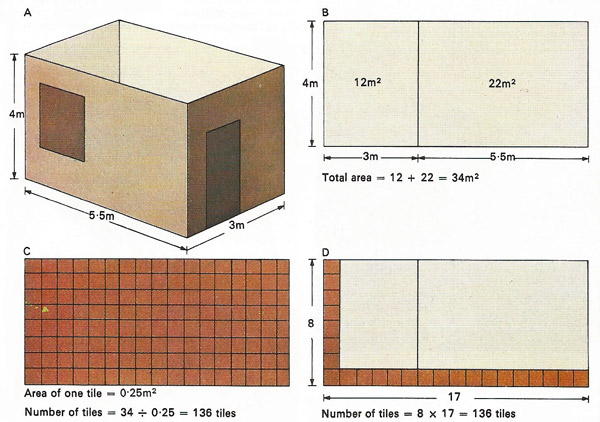
Multiplication and division are needed to solve many everyday problems. A man wants to tile the two main walls of a room [A], which is 5.5 meters long by 3 meters wide and 2 meters tall, using tiles 0.5 meters square. The walls can be drawn [B] as two areas of 22 square meters (m2) and 12 m2, giving a total area of 34 m2. A single tile 0.5 m by 0.5 m has an area of 0.25 m2. The number of tiles required [C] can be found by dividing the area of one tile (0.25 m2). into the total area to be covered (34 m2), giving the result 136 tiles. The same problem can be tackled another way [D]. If the whole area to be tiled is considered it measures 8.5 meters by 4 meters. The long side will accommodate 17 half-meter tiles and the short side only 8 tiles. The total number of tiles required is therefore 17 × 8 = 136, the same result as before but without calculating areas.
Multiplication is a way of combining two numbers to obtain a third; symbolized by ×, ., or merely the juxtaposition of the numbers (where suitable). Where x (the multiplicand) and y are natural numbers, x × y is commutative and defined by x + x + ... + x, the number x appearing y times (see addition).
For multiplication of negative integers, such as (–x) and (–y), (–x).y = x.(–y) = –(x.y); and (–x).(y) = x.y. Multiplication of any number by 0 (see zero) is defined to give the product 0. Fractions may be multiplied by simple extension of the system. The inverse operation of multiplication is division, since x/y = x.(1/y). In cases other than with real numbers, multiplication must be independently defined (see complex number).
Product
A product is the result of one or more multiplications. Thus in a.b = c, the product is c.


