geometry
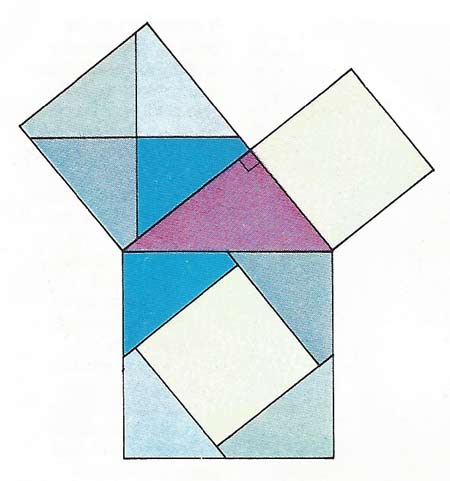
Pythagoras' theorem is the famous one children learn at school. The square on the hypotenuse (the longest side of a right-angled triangle) is the sum of the squares on the other two sides. The big bottom square (the hypotenuse square) divides into four corner sections, which can be reassembled into the top left square, and the one in the center, which is the size of the top right square.
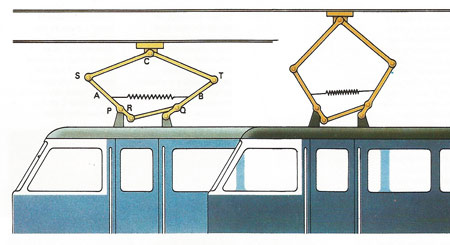
An electric locomotive must always maintain contact with the overhead wire, which itself is not perfectly level. The geometry of the pantograph achieves this. A spring system urges points P and Q together, pivoting arms A and B to shorten distance ST. This distortion of triangle STC keeps C against the overhead wire. As arm A pivots linkage RQ makes B pivot too, preserving symmetry.
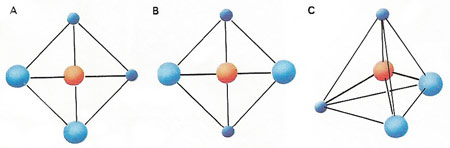
Molecules are too small to be visible so chemists use geometry to deduce molecular structures. Dichloromethane (a solvent used in paint-strippers) has one carbon atom, two hydrogen atoms and two chlorine atoms in its molecule. If they were arranged as a square with the carbon in the middle, two forms of dichloromethane should exist, one with the chlorines adjacent [A] and one with them opposite [B]. But if the atoms are arranged tetrahedrally only one form is possible [C]. Only one form has ever been obtained so the square structure is wrong. By such reasoning chemists deduced the spacial arrangements of thousands of molecules long before methods such as crystallography provided direct evidence.
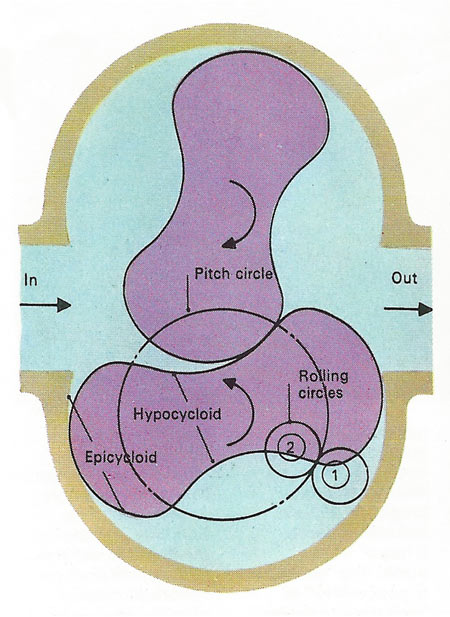
An air compressor uses the subtle geometry of interlinked cycloids. The end-lobes of each "paddle" have the curve traced by a point on a small circle [1] rolling outside the pitch circle. Its waist has the curves from a similar circle [2] rolling on the inside of the pitch circle. As the paddles mesh like 2-toothed cog-wheels, they always touch each other, trapping successive volumes of air and compressing them.
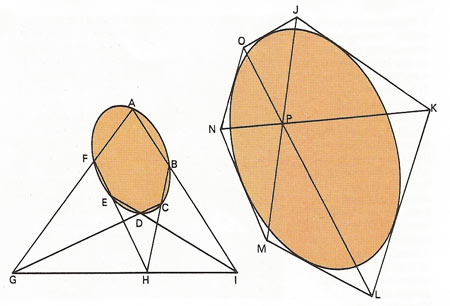
The principle of duality in geometry states that any two lines define a point (their intersection) and any two points define a line (the one joining them). If six points [A-F] touch an ellipse, then the lines joining them form three opposite pairs whose points of intersection meet at a single line [GHI]. The dual of the theorem is that if six lines touch an ellipse then the points at which they intersect [J-O] form three opposite pairs whose lines of connection meet at a single point [P]. So points and lines are "duels" of each other and if these words are interchanged in a theorem, a new theorem results.
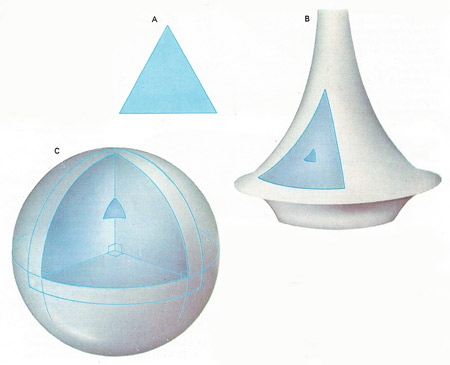
Euclidean geometry [A] is not inevitable and may not be true of real space. Mathematicians accept any geometry that is not self-contradictory and recognise many different kinds. In Lobachevskian geometry [B] the angles never reach 180°, like geometry on a trumpet surface. In Riemann geometry [C] angles of a triangle always exceed the Euclidean 180°, like geometry on the surface of a sphere. Extended to three dimensions this is geometry of 'curved space'.

This model of Felton and Murray's early steam engine is a geometrical theorem in action. The inner cogwheel rolls around a fixed outer gear of twice its diameter. Geometrically, this implies that one point on it reciprocates in an exact straight line. A piston rod attached at this point is driven from a cylinder; a crank takes the drive from the center of the rolling wheel, to drive other machines.
Geometry is the study of the properties of shapes – including lines, curves, and surfaces – and of spaces. Today it is divided into the following main areas:
· algebraic geometry
· analytical geometry
· descriptive geometry
· differential geometry
· Euclidean geometry
· non-Euclidean geometry
· projective geometry
Many of these divisions have grown up only in the last few hundred years.
Introduction
The name geometry is a reminder of its earliest use – for the measurement of land and materials. The Babylonian and Egyptian civilizations thus gained great empirical knowledge of elementary geometric figures, including how to construct a right-angled triangle. The Greek philosophers transformed this practical art into an intellectual pastime through which they sought access to the secrets of nature. About 300 BC Euclid collected together and added to the Greek rationalization of geometry in his Elements. Later Alexandrian geometers began to develop trigonometry. The revival of interest in life-like painting in the Renaissance led to the development of projective geometry, though its is to the philosopher-scientist Decartes that we owe the invention of the algebraic (coordinate) geometry which allows algebraic functions to be represented geometrically. The next new branch of geometry to be developed followed fast upon the invention of calculus: differential geometry.
The greatest upset in the history of geometry came in the 19th century. Men such as Karl Gauss, Nikolai Lobachevsky, and Janós Bolyai began to question the Euclid parallel-lines axiom and discovered hyperbolic geometry, the first non-Euclidean geometry. The elliptical geometry of Bernhard Riemann aided Albert Einstein in the development of the general theory of relativity.
Lines and shapes working for a living
Imagine the United Nations decided to encircle the world at the equator with a steel band symbolizing international unity. If the contractor made it too long by one part in ten million – 4 m in 40,075 kilometers (13 feet in 24,900 miles), how high would it stand above the surface all round the globe? The answer is 63.7 centimeters (about 25 inches).
The foregoing is an example of simple geometry, the mathematics of size and shape. Since all solid objects have size and shape geometry is one of the most practical mathematical studies. If someone wants to know how thick to make a rotating shaft to transmit a certain amount of power, or what contour to give a ship's propeller, or even how much paint is needed to cover a room or concrete to lay a path he uses geometry to provide the solution. Indeed, geometry arose from the surveying needs of the early Egyptians, who had to share out fairly the featureless hectares of fertile mud left by the annual flooding of the River Nile.
The Greeks took geometry over and built an amazing intellectual edifice out of it. Euclid's Elements of Geometry, which was written in about 300 BC, develops a complete "axiomatic system" – a web of interlocking proofs all derived from a few basic axioms. "If you can't prove it, you don't know it!" challenged the Elements and ever since the admitted business of mathematicians has been the clarifying of basic axioms and the proving or disproving of statements derived from them.
A practical engineer seldom bothers with proofs; he generally accepts the mathematician's formulae and uses them. And almost instinctively, he designs objects from rigid parts linked at pivot joints. Many mechanisms around us embody the truths of plane geometry. The motions of a typewriter, the pantograph of an electric locomotive, the suspension of a car, and the linkages in a sewing-machine can all be described as working "models" of a set of geometrical theorems.
Some machines – printing presses and knitting machines for example – appear almost magical in the motions they generate by ingenious geometrical linkages. And most rigid structures use the geometrical fact that a triangle is the only rigid figure. A triangle of rods joined at pivots cannot deform whereas a square, say, can distort to a diamond shape. As a result, girderwork is generally made up of triangles (a big girder bridge is a good example, as is a geodesic dome).
Pi in the sky, and elsewhere
The circle is a simple geometrical shape but one that is mathematically rich. The Greeks succeeded in proving its circumference to be 2πr and its area πr 2, where r is its radius and π some number between 3 1/7 and 3 10/71. In fact π cannot be expressed as any whole-number fraction. Expressed as any whole-number fraction. Expressed in decimals it begins 3.1415926535.... and goes on forever, with a never-ending series of numbers after the decimal point with no numbers repeating. It is a fundamental constant in trigonometry, a numerical branch of geometry invented for mapping the stars and now fundamental to astronomy, navigation, surveying and all kinds of practical measurement. In fact pi has "escaped" from geometry and pervades all numerical measurements.
Some of the most elaborate geometry based on the circle is used in lens design. Almost all lenses - for cameras, spectacles, telescopes and so on – have circular cross-sections. Tracing the light path through a multi-component lens system is a complex geometrical task now carried out by computers. The computer programs calculate the characteristics of many possible lens designs and select the one with the fewest aberrations (for no lens system can be absolutely perfect). The result is a compromise, but the best that can be reached bearing in mind the practical difficulty of actually grinding the lenses.
Solid geometry
Solid geometry is the study of figures in three dimensions. It includes the study of planes intersecting with planes, planes intersecting with solids, solids intersecting with solids, and the measurement of solid figures.
Geometries beyond intuition
Euclidean geometry takes a number of intuitive notions for granted – the idea of a straight line, for example. Euclid thought of it as a line of zero curvature, the shortest line that could be drawn between two points. In practical matters, such as sighting and surveying, we assume that light travels in straight lines. But the physicist feels free to question these suppositions. He considers it possible that light flashed out from the earth might go all round the universe and return to its starting-point, just as a person would who travelled in what he regarded as a "straight line" on the spherical earth. Indeed cosmology, the study of the universe as a whole, currently favors a "closed curved" universe with a finite volume but no boundaries just as the earth's surface has a finite area but is without edges.
Mathematicians see Euclidean geometry as just one of many imaginable geometries, each true of space of a particular curvature. Their theorems may be strange, but provided they can be rigorously derived from the stated axioms (assumed facts), mathematical protocol is satisfied. And which of them is true of our real space is a matter of scientific experiment, not of axiomatic assertion. Fortunately, any curvature must be very small, so that Euclidean geometry works well in the small volumes we can deal with, just as in mapping a small area of the earth it can be assumed to be flat without significant error.

