Arthur Cayley was a British mathematician who published more than 900 papers in pure mathematics. Cayley introduced the concept of a matrix and made important contributions to non-Euclidean geometry and the algebra of matrices. His discoveries in non-Euclidean geometry eventually found their way into the study of the spacetime continuum, whereas his pioneering work in matrices eventually proved crucial in a formulation of quantum mechanics put forward by the German physicist Werner Heisenberg. Cayley was also far ahead of his time in pioneering the idea of abstract groups. He was distantly related to the aviation pioneer George Cayley.

 

Arthur Cayley was born in Richmond, Surrey. He was educated at King's College, London, and Trinity College, Cambridge, and graduated as senior wrangler and first Smith's prizeman in 1842. He was called to the bar at Lincoln's Inn in 1849, and set up a practice as a conveyancer. In 1863 he was elected first Sadlerian Professor of pure mathematics at Cambridge, and in 1875 to a fellowship of Trinity College; and he received honorary degrees from Oxford, Dublin, and Leyden. He was president of the Royal astronomical Society (1872–1873), and of the British Association at its Southport meeting in 1883, where his address on the ultimate possibilities of mathematics attracted much attention. In 1882 he lectured at the Johns Hopkins University, Baltimore, and received the Copley medal of the Royal Society. His chief book was an Elementary Treatise on Elliptic Functions (1876).

 

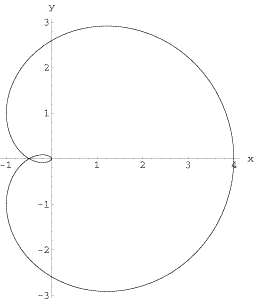
Cayley's sextic

Cayley's sextic is a sinusoidal spiral curve described by the Cartesian equation

 

4(x² + y² - ax)³ = 27a²(x² + y²)²

 

It was discovered by Colin Maclaurin but was first studied in detail by Arthur Cayley and named after him by R. C. Archibald in 1900.

 

 

Cayley's mousetrap

Cayley's mousetrap is a permutation problem invented by Arthur Cayley. Write the numbers 1, 2, ..., n on a set of cards, and shuffle the deck. Now, start counting using the top card. If the card chosen does not equal the count, move it to the bottom of the deck and continue counting forward. If the card chosen does equal the count, discard the chosen card and begin counting again at 1. The game is won if all cards are discarded, and lost if the count reaches n + 1. The number of ways the cards can be arranged such that at least one card is in the proper place for n = 1, 2, ..., are 1, 1, 4, 15, 76, 455, ...