coordinate
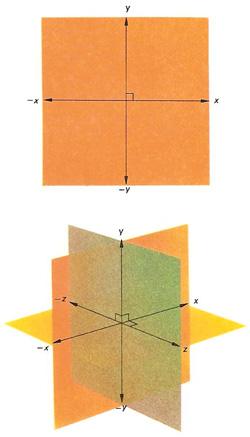
Figure 1. Axes used in rectangular coordinate systems. Those in the top illustration are used in plane geometry, the x-axis being at right angles to the y-axis. Those in the bottom illustration are for use in three dimensions, the x-, y, and z-axes being at mutual right angles.
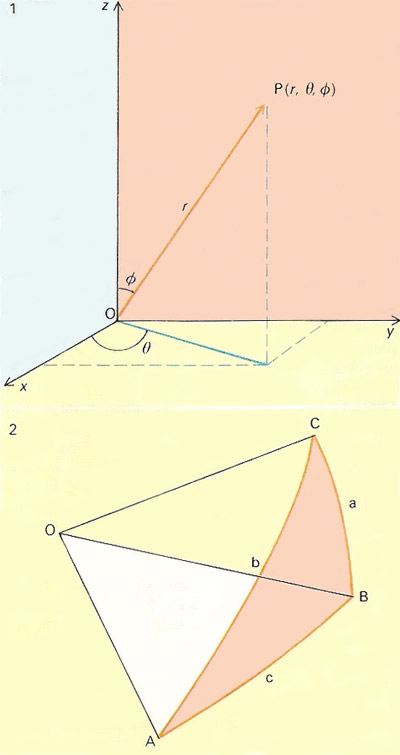
Figure 2. Spherical coordinates.
A coordinate is one of a set of variables that specifies the location of a point in space. If the coordinates are distances measured along perpendicular axes, they are known as Cartesian coordinates. There are many different systems of coordinates in mathematics, astronomy, and science, some of which are described below.
Coordinate systems
Cartesian coordinates
Cartesian coordinates are an ordered set of real numbers that defines the position of a point in terms of its projection on to mutually perpendicular number lines.
Celestial coordinates
Celestial coordinates are any system of coordinates that can be used to give the position of an object, such as a star, on the celestial sphere. A particular system is defined by the chosen point of observation (the origin), the plane of reference, and whether the coordinates are spherical or rectangular.
As an origin, geocentric coordinates use the center of Earth, topocentric coordinates use a specific point on Earth's surface, and heliocentric coordinates use the center of the Sun. This choice of origins can be combined with a variety of reference planes. (1) Equatorial coordinates, the most commonly used in astronomy, may be geocentric or topocentric, and take the celestial equator as their reference plane. (2) Ecliptic coordinates, may be geocentric or heliocentric, and refer to the ecliptic. (3) Horizontal coordinates are topocentric and refer to the observer's horizon. (4) Galactic coordinates are specified relative to the plane of the Galaxy. In all these systems, spherical coordinates dominate but for some special purposes rectangular coordinates are occasionally used.
Cylindrical coordinates
Cylindrical coordinates are a coordinate system in which a point is located by its height z above a reference plane and the polar coordinates of its projection onto that plane, (r, θ). (r, θ, z) can be related to rectangular coordinates by x = r cosθ, y = r sinθ, and z = z (where the original reference plane corresponds to the xy-plane).
Ecliptic coordinates
Ecliptic coordinates are a system that uses the plane of the ecliptic as a reference plane. Ecliptic coordinates of objects with respect to the center of Earth, known as geocentric ecliptic coordinates, are given in terms of celestial latitude (the perpendicular distance of the orbit from the ecliptic in angular measure) and celestial longitude (the angular distance along the ecliptic between the plane through the object and the vernal equinox). Ecliptic coordinates referred to the center of the Sun, known as heliocentric ecliptic coordinates, are given in terms of heliocentric latitude and heliocentric longitude.
Equatorial coordinates
Equatorial coordinates are the most common system of celestial coordinates used by astronomers. Because it takes as a reference plane the plane of the celestial equator (an extension into space of Earth's equatorial plane), it is the sky equivalent of longitude and latitude. Celestial longitude is called right ascension (RA) and is measured eastward along the celestial equator, in hours, minutes, and seconds of sidereal time, or, alternatively, in degrees, starting from 0h (or 0°) at the vernal equinox. Celestial latitude is known as declination (Dec) and is the angular distance of a body north or south of the celestial equator, reckoned positive when north and negative when south. Sometimes, instead of RA and Dec, hour angle and polar distance are used.
Galactic coordinates
Galactic coordinates are coordinates based on the plane of the Milky Way Galaxy, which is inclined about 63° to the celestial equator, and centered on the Sun, with the zero point of longitude and latitude pointing directly at the galactic center. Before 1958, the zero point of galactic latitude and longitude was taken to lie at RA 17h 45.6m, Dec –28° 56.2' (in Sagittarius). Galactic latitude (b) is measured from the galactic equator north (+) or south (-); galactic longitude (l) is measured eastward along the galactic plane from the galactic center.
In 1958, because of increased precision in determining the location of the galactic center, based on observations of the 21-centimeter line, a new system of galactic coordinates was adopted with the origin at the galactic center in Sagittarius at RA 17h 42.4m, Dec –28° 55' (epoch 1950). The new system is designated by a superior Roman numeral II (i.e., bII, l II) and the old system by a superior Roman numeral I.
Heliocentric coordinates
Heliocentric coordinates is a system of celestial coordinates that has its origin at the center of the Sun and takes the ecliptic as its plane of references. Heliocentric coordinates are used especially in calculations of the relative positions of the planets and other bodies of the Solar System.
Heliographic coordinates
Heliographic coordinates are the latitude and longitude of a feature on the Sun's surface. Heliographic latitude is an object's angular distance north or south of the solar equator; heliographic longitude can be measured east or west of the central solar meridian, or given in terms of the Carrington rotation number.
Horizontal coordinates
Horizontal coordinates are a system of celestial coordinates that uses the observer's horizon as a reference plane and the observer's latitude and longitude as a point of origin. The position of a star, or other object, on the celestial sphere, at any given time, is determined by its altitude, the angular distance of the object above the horizon, and its azimuth, the angular distance of the object angle measured east from north and parallel to the horizon.
Polar coordinates
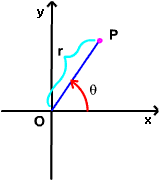
Polar coordinates are a coordinate system in which distances are measured from a fixed reference point (the pole), and angles from a fixed reference line. There are two polar coordinations, r and θ, of a point P in the plane, where r is the point's distance from the origin and θ is an angle measured anticlockwise from some reference line emanating from the origin. Spherical polar coordinates incorporate a second angle, φ, which represents the angle of inclination of a line drawn to the point from a plane surface.
A polar equation is one that uses polar coordinates.
 |
Rectangular coordinates
Rectangular coordinates are a set of coordinates that gives the position of an object with respect to two or three mutually perpendicular axes (x, y, and z) that cross at some specified origin (see Figure 1). In astronomy, heliocentric or geocentric rectangular coordinates are occasionally used to give positions of bodies in the Solar System.
Spherical coordinates
Spherical coordinates are a system for specifying positions in terms of angles on a sphere, such as the celestial sphere or the surface of a planet or large moon (Figure 2). In spherical coordinates, a point P in space is located by its position relative to three mutually perpendicular axes (the x-, y-, and z-axes) in terms of (1) its distance r from the origin, O, (2) the angle (θ) between the x-axis and the projection of OP onto the x-y plane, and (3) the angle (φ) between OP and the z-axis. The coordinates of P are thus expressed in the form (r, θ, φ). See also analytic geometry.
In the accompanying diagram, a spherical coordinates system is shown defining point P in terms of distance r and angles θ and φ. (2) The spherical triangle ABC has "sides" a, b, c which are the angles BOC, AOC, and AOB respectively and "angles" A, B, C where A is the angle between the tangents to the arcs AC and AB at A; B that between the tangents to the arcs AB and BC at B; and C that between the tangents to the arcs AC and BC at C respectively.
 |
Topocentric coordinates
Topocentric coordinates is a system of celestial coordinates with its origin at a specific point on Earth's surface. Usually, the difference in the position of an object in the sky measured using topocentric and geocentric (Earth-centered) coordinates is very small because most celestial objects are so far away. The Moon's position, however, can vary as much as 2° depending on where on Earth it is measured from, and, within the past few years, an observatory in Australia missed spotting an asteroid that passed close to Earth because it used geocentric rather than topocentric positions.


