hadron
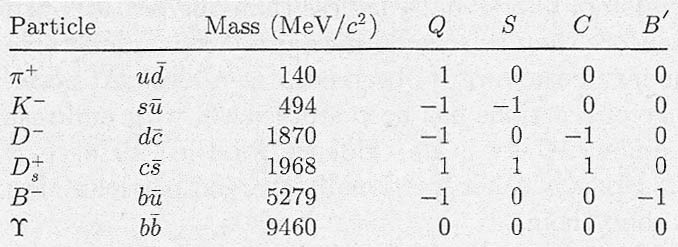
Table 1. Approximate values of quark masses in units of GeV/c 2 and their electric charges Q in units of e. Also shown are the values of the quantum numbers: baryon number B, strangeness S, charm C, bottom B', and top T. Their values, and those of Q, for the corresponding antiquarks are in magnitude, but opposite in sign.
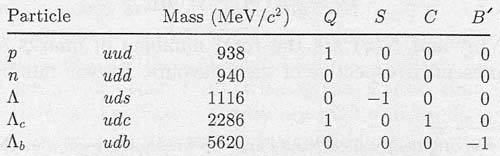
Table 2. Some examples of baryons, with their compositions, and the corresponding values of their electric charge Q, strangeness S, charm C, and bottom B'.
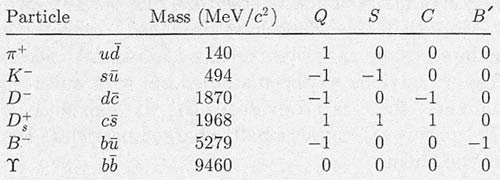
Table 3. Some examples of baryons, with their compositions, and the corresponding values of their electric charge Q, strangeness S, charm C, and bottom B'.
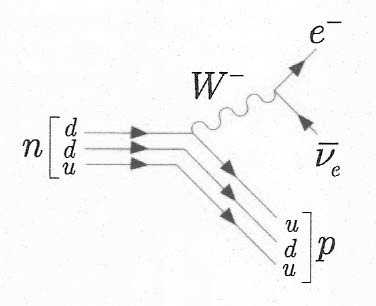
Figure 1. Quark diagram for the decay: n → p + e– + νe.
A hadron is any particle made of quarks and gluons. Hadrons include mesons, which are quark doublets, and baryons (such as the proton and neutron), which are quark triplets. Hadrons can interact via the strong force. Although they have no overall strong charge (i.e., they are strong charge neutral objects) they take part in residual strong interactions due to the strong charges of their constituents.
The name "hadron" comes from the Greek for "thick and bulky" and was coined by the Russian physicist L. Okun in 1962.
General properties of hadrons
Although no isolated quarks have been found, well over two hundred of their bound states have been discovered, all with integer electric charges. The reason for the latter is closely associated with a degree of freedom that exists for quarks, but not for leptons, called color. Here, though, we'll follow a simple quark model in assuming that only the three simplest types of quark bound states with integer electric charge need be considered. These are the baryons, which have half-integer spin and are assumed to be bound states of three quarks (qqq); the antibaryons, which are their antiparticles and assumed to be bound states of three antiquarks (q̅q̅q̅); and the mesons, which have integer spin and are assumed to be bound states of a quark and an antiquark (qq̅). Some examples of baryons and mesons, together with their quark compositions, are shown in Tables 2 and 3, which also show the values of several quantum numbers that are associated with any state and that refer to its quark content. For example, the strangeness S is defined by
where N(s) and N(s̅) are the number of s quarks and s̅ antiquarks present in the state. Clearly S = –1 for an s quark, S = 1 for an s̅ antiquark and S = 0 for all other quarks and antiquarks. The charm (C), bottom (B' ), and top (T) quantum numbers are similarly defined by
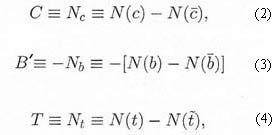 |
respectively, giving values for the individual quarks, which are summarized Table 1.
The resulting values of S, C, and B' for our specimen hadrons are given in Tables 2 and 3 together with the hadron's electric charge Q, which is just the sum of the appropriate quark charges. The top quantum number T = 0 for all known hadrons. The remaining quark numbers,
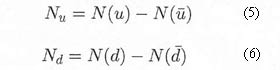 |
do not have special names since, given S, C, B', T, and Q, their values can be inferred from the baryon number B of the state, defined by
where N(q) and N(q̅) are the total numbers of quarks and anti-quarks present, irrespective of their flavors. The baryon number B = 1 for baryons, B = –1 for antibaryons, and B = 0 for mesons. In terms of the quark numbers (equations 1–6)
while the electric charge is given by
All these quantum numbers are called internal quantum numbers because they are not associated with motion or the spatial properties of wave functions. They are important because in strong and electromagnetic interactions quarks and antiquarks are only created or destroyed in particle-antiparticle pairs. For example, the quark description of the strong interaction process
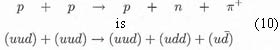 |
On counting the quarks of each flavor, we see that the final state contains the same number of quarks of each flavor as the initial state, plus an additional (dd̅), so that the quark numbers Nu and Nd are separately conserved. This is characteristic of strong and electromagnetic processes, in which all the quark numbers (1–9) are separately conserved. However, in neutron β decay,
whose quark interpretation is
where a d-quark is replaced by a u-quark. This decay is represented by the quark diagram of Figure 1. The fact that Nu and Nd are not conserved is characteristic of the weak interactions, in which the quark flavors can change and only the baryon number (7) and the total electric charge are in general conserved.
The quark numbers (equations 1–9) play an important role in understanding the long lifetimes of some hadrons. Hadrons have typical effective radii r of order 1 fm, with an associated time scale r/c of order 10–23 second. The vast majority are highly unstable, and decay to lighter hadrons by the strong interaction with lifetimes of this order. However, each hadron is characterized by a set of values for B, Q, S, C, B', and T, and in some cases there are no lighter hadron states with the same values of these quantum numbers to which they can decay. These hadrons, which cannot decay by strong interactions, are long-lived on a timescale of order 10–23 second and are often called stable particles. Here we shall call them long-lived particles, because except for the proton they are not absolutely stable, but decay by either the electromagnetic or weak interaction. Electromagnetic decay rates are suppressed by powers of the fine structure constant a relative to strong decays, leading to observed lifetimes in the range 10–16–10–21 second. Weak decays give longer lifetimes that depend sensitively on the characteristic energy of the decay). A useful measure of this characteristic energy is the Q value, which is the kinetic energy released in the decay of the particle at rest. For neutron decay (11),
and the lifetime is about 103s. However, Q values of order 102–103 MeV are more typical, and the observed lifetimes for other weak hadron decays lie in the range 10–7–10–13 second. Thus hadron lifetimes span some 27 orders of magnitude, from about 10–24 second to about 103 second.
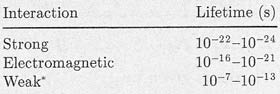 |
| Typical lifetimes of hadrons decaying by the three interactions. * The neutron lifetime is an exception. |


